乱数を使ってサイコロを作ってみます。
1~6の出目の特徴を、numpyとmatplotlibで視覚化してみましょう。
乱数とは
乱数は、まったく規則性がなく、同じ確率で現れる数字の並びのことです。
コンピューターで生成する乱数は、計算によって求めているため、規則性や再現性がある疑似乱数です。
課金システムのガチャや、暗号で使用するときには注意が必要ですが、この記事は乱数の使い方としてご覧ください
乱数を生成する関数
Pythonの標準ライブラリには、疑似乱数を生成するrandomモジュールが用意されています。
random.randrange(start, stop[,step])
range(start, stop, step)の要素からランダムに選ばれた要素を返します。
range関数と同じで、startとstepは省略できます。
import random
random.randrange(10)6range(10)は、0から9までの整数を返すので、この例では0から9までの乱数が生成されます。
range関数の詳しい使い方は、以下の記事をご覧ください。
>>【Python入門】range関数の使い方(for文で繰り返し処理)
random.randint(a, b)
a <= N <= b となるような整数をランダムに返します。
random.randrange(a, b+1)と同じです。
randint関数は、bで指定した値を含む点に注意してください。
random.seed(a=None)
randomモジュールの関数は、呼び出される毎に違う値を生成します。
seed()のaを省略するか、Noneを指定すると、乱数シード(種)に、現在のシステム時刻が使用されます。
現在のシステム時刻は常に異なっているため、違う値が生成されます。
機械学習などで、同じ乱数を生成したいときは、乱数シードを固定します。
random.seed(0)
for i in range(5):
print(random.randrange(10))6
6
0
4
8乱数シードを0に固定しています。
このコードは何度実行しても、同じ値が生成されます。
random.choices(population, weights=None, k=1)
choices関数は、ランダムに値を選択することで、乱数列を生成することができます。
populationで指定した要素から重複ありで大きさkのリストを返します。
import random
Number = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
random.choices(Number, k=5)[7, 6, 1, 0, 0] パラメーターweightsを指定すると、相対的な重みが設定できます。
populationの要素が2つのとき、weights=[3, 1]と指定すると、1つ目の要素が選択される確率が3倍になります。
import random
zeroich = [0, 1]
random.choices(zeroich, weights=[3, 1], k=5)[1, 0, 0, 0, 0]いかさまサイコロの作成
サイコロの出目は、1から6まで規則性なく、同じ確率で現れるものです。
丁半ばくちのように、2個のサイコロで出目を可視化してみます。
まずは、偏りのない普通のサイコロを作成します。
普通のサイコロ
2個のサイコロを振り、出目を6×6のマス目でカウントします。
出目が[1, 1]だと左上、出目が[6, 6]なら右下。
5000回振ってみると、確率的には5000回÷36マスで、1マスあたり139回となるはずです。
random.randint()で作成
各マスを0で初期化。カウントが増えるごとに黒くなります。
0が白。255が黒。中間が灰色。として可視化します。
import numpy as np
import matplotlib.pyplot as plt
import random
img = np.zeros([6, 6])
print(img)
plt.imshow(img, cmap='Greys') [[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]]
numpy配列を、0で初期化しました。
サイコロの出目1~6を、numpy配列の0~5にカウントします。
すべて0なので、真っ白な画像になります。
numpy配列を画像して扱う方法は、以下をご覧ください。
>>【Python入門】機械学習の前処理(画像処理のやり方)
それでは、サイコロを振ってみます。
img = np.zeros([6, 6])
random.seed(0)
for i in range(5000):
img[random.randint(0, 5), random.randint(0, 5)] += 1
print(img)
plt.imshow(img, cmap='Greys') [[147. 139. 146. 148. 140. 150.]
[128. 152. 141. 141. 142. 134.]
[125. 136. 139. 148. 139. 142.]
[122. 125. 166. 134. 145. 129.]
[128. 153. 138. 137. 119. 148.]
[136. 147. 137. 128. 124. 147.]]
まだら模様の画像になりました。
乱数シードを0に指定しているので、このコードはいつ実行しても同じ結果になります。
[横軸, 縦軸]として、[2, 3]のマスが166回でたのが最多で、[4, 4]のマスが119回で最少です。
視覚的には、均等な出目なのか判断に迷うので、統計値を取ってみます。
import pandas as pd
img_dice = pd.Series(img.reshape(-1)) # numpy配列を1次元にして、Seriesに変換
img_dice.describe()count 36.000000
mean 138.888889
std 10.152488
min 119.000000
25% 132.750000
50% 139.000000
75% 147.000000
max 166.000000
dtype: float64結果は、平均値(mean)138.888889 ± 標準偏差(std)10.152488
均等な出目が139回なので、概ね予想どおりの結果が期待できそうです。
同じ試行を10000回繰り返してみます。
numpy配列が3次元になります。
img = np.zeros([6, 6, 10000])
random.seed(0)
for i in range(10000):
for j in range(5000):
img[random.randint(0, 5), random.randint(0, 5), i] += 1
print(img[:, :, 0])
plt.imshow(img[:, :,0], cmap='Greys') 結果の表示は省略しますが、コードは1回目の試行を表示します。
乱数シードを0に指定しているので、1回目の結果は先ほどと同じです。
同じコードを使用して統計値を見てみましょう。
count 360000.000000
mean 138.888889
std 11.628179
min 88.000000
25% 131.000000
50% 139.000000
75% 147.000000
max 193.000000
dtype: float64結果は、平均値(mean)138.888889 ± 標準偏差(std)11.628179
たくさん試行したので、発生する値の幅が広くなったようです。
ヒストグラムで見てみましょう。
plt.hist(img_dice, bins=105);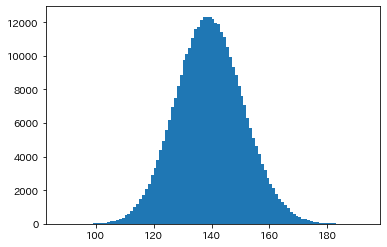
平均値139を頂点とした正規分布をしています。
均等な出目になるケースが一番多く、極端な出目(よく出る出目、あまり出ない出目)になるケースになるにつれて少なくなっています。
ヒストグラムのbinsは、縦棒に割る数を指定します。
今回は、最小値から最大値まで整数値になるように指定しています。
random.choices()で作成
random.randint()は、乱数を作りながらカウントしました。
random.choices()は、あらかじめ乱数列を作成し、リストから呼び出します。
img = np.zeros([6, 6, 10000])
random.seed(0)
Dice = [0, 1, 2, 3, 4, 5]
for j in range(10000):
dice1 = random.choices(Dice, k=5000)
dice2 = random.choices(Dice, k=5000)
for i in range(5000):
img[dice1[i], dice2[i], j] += 1
print(img[:, :, 0])
plt.imshow(img[:, :, 0], cmap='Greys') [[142. 135. 143. 138. 135. 143.]
[126. 123. 131. 118. 141. 124.]
[143. 153. 137. 134. 164. 138.]
[140. 152. 131. 155. 161. 116.]
[134. 169. 127. 139. 135. 132.]
[135. 134. 157. 152. 119. 144.]]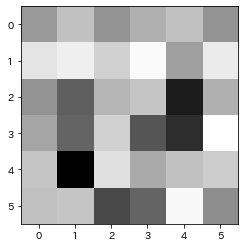
import pandas as pd
img_dice = pd.Series(img.reshape(-1))
img_dice.describe()count 360000.000000
mean 138.888889
std 11.627274
min 91.000000
25% 131.000000
50% 139.000000
75% 147.000000
max 197.000000
dtype: float64結果は、平均値(mean)138.888889 ± 標準偏差(std)11.627274
random.randint()の結果とほぼ同じです。
ヒストグラムでも確認しておきましょう。
plt.hist(img_dice, bins=106);
random.choices()は、あらかじめ乱数列を作成するので、random.randint()より処理が速いです。
あらかじめ処理する量がわかっているときは、random.choices()をおすすめします。
jupyter notebookなら、セルの初めに「%%time」で処理時間が測れます。
偏りのあるサイコロ
本題のいかさまサイコロを作成します。
random.choices()のパラメーターweightsを設定します。
偶数の出目[2, 4, 6]に重みを、1より大きくしてみます。
numpy配列では、[1, 3, 5]なので注意してください。
img = np.zeros([6, 6, 10000])
random.seed(0)
Dice = [0, 1, 2, 3, 4, 5]
for j in range(10000):
dice1 = random.choices(Dice, weights=[1, 1.2, 1, 1.5, 1, 1.3], k=5000)
dice2 = random.choices(Dice, weights=[1, 1.2, 1, 1.5, 1, 1.3], k=5000)
for i in range(5000):
img[dice1[i], dice2[i], j] += 1
print(img[:, :, 0])
plt.imshow(img[:, :, 0], cmap='Greys') [[104. 116. 100. 164. 101. 133.]
[114. 133. 118. 163. 116. 145.]
[102. 125. 109. 145. 116. 153.]
[150. 199. 152. 236. 177. 175.]
[103. 143. 89. 158. 88. 138.]
[131. 159. 145. 211. 120. 169.]]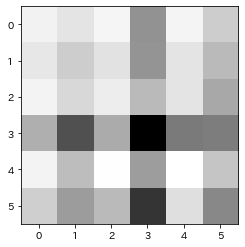
これは、視覚的にも偏りがあることがわかります。
統計値とヒストグラムでも確認してみましょう。
結果のみを掲載しますので、コードは前述を確認ください。
count 360000.000000
mean 138.888889
std 33.977592
min 60.000000
25% 113.000000
50% 134.000000
75% 159.000000
max 291.000000
dtype: float64結果は、平均値(mean)138.888889 ± 標準偏差(std)33.977592
出目のバラツキは大きくなっていますが、平均値は同じです。
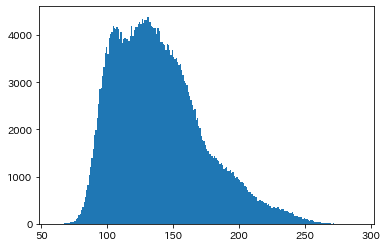
すごく出る目(159回以上)が増え、あまり出ない目(113回以下)も増えています。
weightsなしとweightsありのグラフを重ねてみると、違いがよくわかります。
plt.figure()
plt.hist(img_dice, bins=106, alpha=0.3, color='r') # weightsなし
plt.hist(img_dice_weights, bins=231, alpha=0.3, color='b') # weightsあり
plt.show()
weightsなしが赤。weightsありが青。
平均値は同じですが、バラツキの大きさがまったく違っています。
グラフを使った視覚化は効果的ですが、作り方次第でまったく違う印象を与えることになります。
また、実は平均値は使用する乱数の数によって決定しています。
均等な出目であれば1マスに139回×36マスですが、どんなに出目が偏っていても、各マスの合計は同じ5000回なので、平均値は139回になります。
平均値だけでは、データの特徴を判断できないことがよくわかります。
まとめ
- 乱数の使い方がわかった
- numpy配列を、グレースケール画像として視覚化することができた
- 3次元のnumpy配列で、複数の画像を重ね合わせることができた
- 作成したデータの特徴を、統計量とグラフを使って確認することができた


