「【Python覚書】LigthGBMで多値分類問題を解いてみる」の続編として、交差検証を解説します。
この記事だけで動くコードになっていますが、時間が許すようなら、以下もご覧ください。
【Python覚書】LigthGBMで多値分類問題を解いてみる
特徴量の作成まで
# モジュールのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import lightgbm as lgb
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.model_selection import StratifiedKFold
# iris データセットを読み込む
iris = datasets.load_iris()
X = iris['data']
y = iris['target']
# 説明変数をpandas.DataFrameに入れ、カラム名を付ける
df_X = pd.DataFrame(X, columns=iris['feature_names'])
# カテゴリー変数を作成
# sepal(がく)の面積から4区分のカテゴリーを作成
df_X['sepal_cat'] = df_X['sepal length (cm)'] * df_X['sepal width (cm)']
df_X['sepal_cat'] = pd.qcut(df_X['sepal_cat'], 4, labels=False)
df_X['sepal_cat'] = df_X['sepal_cat'].astype('category')
# カテゴリー変数を作成
# petal(花びら)の面積から4区分のカテゴリーを作成
df_X['petal_cat'] = df_X['petal length (cm)'] * df_X['petal width (cm)']
df_X['petal_cat'] = pd.cut(df_X['petal_cat'], 4, labels=False)
df_X['petal_cat'] = df_X['petal_cat'].astype('category')交差検証
ホールドアウト法(holdout cross-validation)

ホールドアウト法については、こちらの記事をご覧ください。
ホールドアウト法の解説
K分割交差検証(K-fold cross-validation)
・学習データの使い方
K分割交差検証は、学習データをK個のフォールド(fold)に分割し、そのうちの1つを検証に使用し、残りを学習に使用します。
5分割交差検証では、5通りの分割を行い、5回の学習と検証を行うことで、5個のモデルを作ることができます。
・テストデータの使い方
K分割交差検証では、K個のモデルが作られます。
それぞれのモデルを、テストデータで性能評価することで、モデルの平均性能がわかります。
5分割交差検証を例にとると、それぞれのモデルで推定した成績の平均値を求めます。
10点を満点とするモデルでは、(8+10+9+7+6) / 5 = 8 として、8点が平均性能となります。
・ポイント
モデルの学習は、学習データを学習用と検証用に分割して行いますが、データの分け方によって、モデルの性能に違いができます。
モデルは学習の過程で、検証用のデータでよい成績がでるようにパラメータが調整されていきます。
結果として、検証用のデータとテストデータの特徴が近いと、テストデータでもよい成績になりますが、これでは性能が運まかせになってしまいます。
その解決策として、K分割交差検証のように複数のモデルの平均を使うことで、どのようなテストデータに対しても、そこそこよい成績が出せるようにします。
これを、汎化性能を高めると呼んでいます。
モデルの作成
モデルの作成を、次のステップで行います。
1. 特徴量と目的変数を、LightGBM用のデータ構造に変換
2. ハイパーパラメーターの設定
3. 学習の実行
特徴量と目的変数を、LightGBM用のデータ構造に変換
まずは、データを2つに分けます。
・学習データ → モデルの作成
・テストデータ → モデルの性能評価
# 学習データとテストデータに分ける
X_train, X_test, y_train, y_test = train_test_split(df_X, y,
test_size=0.2,
random_state=0,
stratify=y)学習の実行
学習データを使用して、モデルを作成します。
5分割交差検証を行うので、5通りの分割を行い、5回の学習と検証を行うことで、5個のモデルを作ります。
作成したモデルは、リストに保存して、後で使用します。
また、モデルを作成するごとに、各モデルの性能を表示します。
パラメータは決め打ちで行いますが、学習率を変化させると、学習過程が大きく変わりますので、試してみてください。
# カテゴリー変数
categorical_features = ['sepal_cat', 'petal_cat']
# 5-fold CVモデルの学習
# 5つのモデルを保存するリストの初期化
models = []
# 学習データの数だけの数列(0行から最終行まで連番)
row_no_list = list(range(len(y_train)))
# KFoldクラスをインスタンス化(これを使って5分割する)
K_fold = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)
# KFoldクラスで分割した回数だけ実行(ここでは5回)
for train_cv_no, eval_cv_no in K_fold.split(row_no_list, y_train):
# ilocで取り出す行を指定
X_train_cv = X_train.iloc[train_cv_no, :]
y_train_cv = pd.Series(y_train).iloc[train_cv_no]
X_eval_cv = X_train.iloc[eval_cv_no, :]
y_eval_cv = pd.Series(y_train).iloc[eval_cv_no]
# 学習用
lgb_train = lgb.Dataset(X_train_cv, y_train_cv,
categorical_feature=categorical_features,
free_raw_data=False)
# 検証用
lgb_eval = lgb.Dataset(X_eval_cv, y_eval_cv, reference=lgb_train,
categorical_feature=categorical_features,
free_raw_data=False)
# パラメータを設定
params = {'task': 'train', # 学習、トレーニング ⇔ 予測predict
'boosting_type': 'gbdt', # 勾配ブースティング
'objective': 'multiclass', # 目的関数:多値分類、マルチクラス分類
'metric': 'multi_logloss', # 分類モデルの性能を測る指標
'num_class': 3, # 目的変数のクラス数
'learning_rate': 0.02, # 学習率(初期値0.1)
'num_leaves': 23, # 決定木の複雑度を調整(初期値31)
'min_data_in_leaf': 1, # データの最小数(初期値20)
}
# 学習
evaluation_results = {} # 学習の経過を保存する箱
model = lgb.train(params, # 上記で設定したパラメータ
lgb_train, # 使用するデータセット
num_boost_round=1000, # 学習の回数
valid_names=['train', 'valid'], # 学習経過で表示する名称
valid_sets=[lgb_train, lgb_eval], # モデル検証のデータセット
evals_result=evaluation_results, # 学習の経過を保存
categorical_feature=categorical_features, # カテゴリー変数を設定
early_stopping_rounds=20, # アーリーストッピング# 学習
verbose_eval=-1) # 学習の経過の非表示
# テストデータで予測する
y_pred = model.predict(X_test, num_iteration=model.best_iteration)
y_pred_max = np.argmax(y_pred, axis=1)
# Accuracy を計算する
accuracy = sum(y_test == y_pred_max) / len(y_test)
print('accuracy:', accuracy)
# 学習が終わったモデルをリストに入れておく
models.append(model) 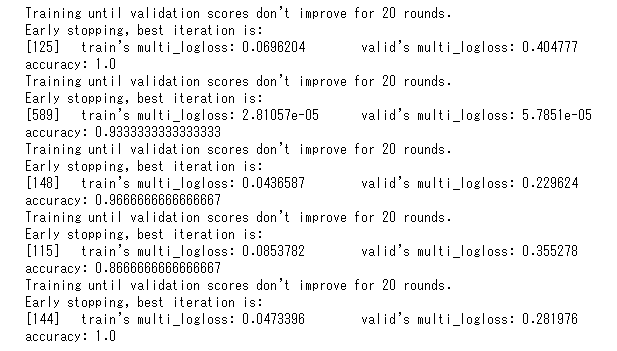
モデルの評価
5分割交差検証で、5つのモデルを作成しました。
表にまとめると、以下のようになりました。
| 学習用 | 検証用 | 正答率 | |
| 1回目 | 0.0696204 | 0.404777 | 1.0000 |
| 2回目 | 0.0281057 | 0.578510 | 0.9333 |
| 3回目 | 0.0436587 | 0.229624 | 0.9666 |
| 4回目 | 0.0853782 | 0.355278 | 0.8666 |
| 5回目 | 0.0473396 | 0.281976 | 1.0000 |
学習用と検証用の列は、multi Loglossなので、0~1の確率の値を取ります。
この値が小さく(0に近く)なるように、パラメータがチューニングされます。
このモデルでは、検証用の数値が改善しなくなると学習が止まります。(アーリーストッピング)
学習の過程を見てみます。
# 学習過程の可視化
plt.plot(evaluation_results['train']['multi_logloss'], label='train')
plt.plot(evaluation_results['valid']['multi_logloss'], label='valid')
plt.ylabel('Log loss')
plt.xlabel('Boosting round')
plt.title('Training performance')
plt.legend()
plt.savefig('cv_logloss.jpg')
plt.show()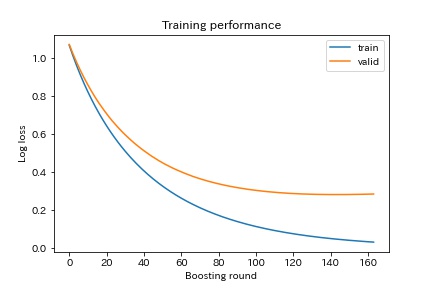
上のグラフは、5回目の学習過程でのLoglossで、学習用がtrain、検証用がvalidです。
validが最も値のよい144回目の学習から20回改善しなかったので、164回目で学習が止まっています。
学習用と検証用がかなりの乖離しているので、過学習ぎみでしょうか。
元の表に戻って、正答率は4回目が0.8666と低く、1回目と5回目は1.0なので完全に正解しています。
このように、同じモデルでも学習に使用するデータで性能が違ってきます。
モデルのアンサンブル
今回は5つのモデルを作成したので、これを融合させた1つのモデルとして予測を行います。
LightGBM以外のロジスティック回帰や決定木などと組み合わせて、より汎化性能を高める例がありますが、今回はシンプルにLightGBMの5つのモデルを融合させます。
<融合の手順>
・各モデルで予測(3つに分類する問題なので、種類ごとの確率を出力)
例、1行目が、0の確率90%、1の確率8%、2の確率2% ← 計100%になるよう予測
・5つのモデルの値を平均し、最も確率大きい種類を答えとする
| (例) | 0 | 1 | 2 |
| 1回目 | 90% | 8% | 2% |
| 2回目 | 95% | 3% | 2% |
| 3回目 | 80% | 5% | 15% |
| 4回目 | 40% | 30% | 30% |
| 5回目 | 20% | 30% | 50% |
| 平均 | 65.0% | 15.2% | 19.8% |
上の例だと、0列の確率の平均が最も大きくなるので、0を答えと予測します。
なお、今回はモデルの出力値が同じため、値の平均で予測していますが、分類のアンサンブルは、投票数(0を答えとするモデルの数)による多数決で答えを決めことが多いです。
それでは、コードを見てみましょう。
# テストデータ格納用のnumpy行列を作成
test_pred = np.zeros((len(y_test), 3, 5))
# 5個のモデル
for fold_, model in enumerate(models):
# testを予測
pred_ = model.predict(X_test, num_iteration=model.best_iteration)
# testの予測を保存
test_pred[:, :, fold_] = pred_
# テストデータで予測する
y_pred = np.zeros((len(y_test), 3))
y_pred[:, 0] = np.mean(test_pred[:, 0, :], axis=1)
y_pred[:, 1] = np.mean(test_pred[:, 1, :], axis=1)
y_pred[:, 2] = np.mean(test_pred[:, 2, :], axis=1)
y_pred_max = np.argmax(y_pred, axis=1)
# Accuracy を計算する
accuracy = sum(y_test == y_pred_max) / len(y_test)
print('accuracy:', accuracy)accuracy: 0.9666666666666667正答率0.9666となり、5つのモデルの平均ぐらいになりました。
テストデータが30個で、1個のみ間違っています。
誤答の確認
誤答になったテストデータに、各モデルは以下のように予測しています。
答えは、2です。
| 0 | 1 | 2 | |
| 1回目 | 33.3% | 33.3% | 33.3% |
| 2回目 | 0.0% | 100.0% | 0.0% |
| 3回目 | 33.3% | 33.3% | 33.3% |
| 4回目 | 25.9% | 48.2% | 25.9% |
| 5回目 | 33.0% | 33.0% | 34.0% |
| 平均 | 25.1% | 49.6% | 25.3% |
5回目のモデルが正答を予測していますが、自信をもった答えではないようです。
他のモデルもあいまいな答えですが、実は1回目と2回目も小数点以下15桁までいくと、2の正答を予測しています。
このデータは、値の平均により分類したために誤答になっており、投票数で分類すると正答します。
投票による分類
コードを少し手直しして、投票での予測をしてみます。
投票数にするため、最も確率が高い種類を1、他を0とします。
上の誤答の場合は、以下のような投票となり、正答の2を予測できます。
| 0 | 1 | 2 | |
| 1回目 | 0 | 0 | 1 |
| 2回目 | 0 | 1 | 0 |
| 3回目 | 0 | 0 | 1 |
| 4回目 | 0 | 1 | 0 |
| 5回目 | 0 | 0 | 1 |
| 票数 | 0票 | 2票 | 3票 |
確率を投票する分類に変換するコードを追記します。
# テストデータ格納用のnumpy行列を作成
test_pred = np.zeros((len(y_test), 3, 5))
# 5個のモデル
for fold_, model in enumerate(models):
# testを予測
pred_ = model.predict(X_test, num_iteration=model.best_iteration)
# testの予測を保存
test_pred[:, :, fold_] = pred_
# ここから追記
# モデルの予測を確率から分類に変換
# コピーする必要はないが、変更を分かりやすくするため
test_pred_copy = test_pred.copy()
# テストデータの行
for i in range(len(y_pred)):
# 各モデル
for j in range(5):
a = test_pred_copy[i, :, j]
# 最大値の列番号
test_pred_copy_max = np.argmax(a)
# 最大値の列を1、他を0
if test_pred_copy_max == 0:
test_pred_copy[i, 0, j] = 1
test_pred_copy[i, 1, j] = 0
test_pred_copy[i, 2, j] = 0
elif test_pred_copy_max == 1:
test_pred_copy[i, 0, j] = 0
test_pred_copy[i, 1, j] = 1
test_pred_copy[i, 2, j] = 0
elif test_pred_copy_max == 2:
test_pred_copy[i, 0, j] = 0
test_pred_copy[i, 1, j] = 0
test_pred_copy[i, 2, j] = 1
# ここまで追記(以下は、test_pred_copyを使用)
# テストデータで予測する
y_pred = np.zeros((len(y_test), 3))
y_pred[:, 0] = np.sum(test_pred_copy[:, 0, :], axis=1)
y_pred[:, 1] = np.sum(test_pred_copy[:, 1, :], axis=1)
y_pred[:, 2] = np.sum(test_pred_copy[:, 2, :], axis=1)
y_pred_max = np.argmax(y_pred, axis=1)
# Accuracy を計算する
accuracy = sum(y_test == y_pred_max) / len(y_test)
print('accuracy:', accuracy)accuracy: 1.0正答率1.0となり、すべてのデータを正しく分類できるようになりました。
今回は、投票数による多数決のほうがよい成績になるようです。
まとめ
交差検証の解説書は、結構さらっとしている印象で、初心者に優しくないと思っています。
また、データの量によっては、計算にそこそこの時間がかかるので、動かしながらの勉強が難しい面もあります。
今回使用したのirisデータセットは、データ量が少ない分、計算は軽いので、とりあえず動かしてみてください。
その後、もっと大きなデータセットを使用して、パラメータのチューニングなどを行ってみると、交差検証の効果がよくわかると思います。


