気温は、昼に上がり、夜に下がる、時刻の周期性に関連をもった特徴量と言えます。
そのような周期性をもった時系列データを、線形モデルで予測してみましょう。
使用するライブラリ
# 使用するライブラリ
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.linear_model import RidgeCV線形モデルは、リッジ回帰で、交差検証を行う「RidgeCV」を使用します。
使用するデータ
気象データの取得
気象庁のWebサイトから、2020年4月の練馬の気象データを取得しました。
使用しない項目を整理した、以下のファイルを使用します。
公式サイト: 気象庁 過去の気象データ検索
ここでは、Pandasを使って、直接Web上(このサイト)から取り込みます。
コードの解説は、次の記事をご覧ください。
【Python入門】CSVファイルをコード1行で読み込む方法
# CSVファイルを、Pandasデータフレームに取り込む
df_web = pd.read_csv( filepath_or_buffer='https://potesara-tips.com/wp-content/uploads/2021/02/temperature.csv',
sep=',', header=0, index_col=None, encoding='cp932')
# Pandasデータフレームを表示
display(df_web)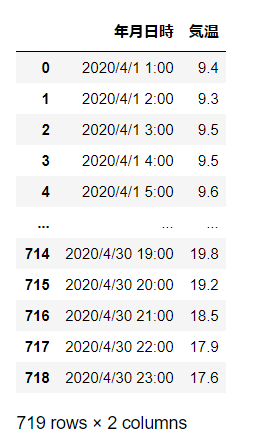
4月ひと月分の、1時間ごとの気温を取得しました。
30日 * 24H = 720行ではないのは、4月1日の0時がないためで、
1行少ない719行です。
データの前処理
列名「年月日時」を、日付データのdatetime64型に変換
列名「年月日時」を、日付データのdatetime64型に変換することで、日付として取り扱いが便利になります。
Pandasの「to_datetime()」を使用します。
第1引数で「値」、第2引数で「書式」を指定しています。
標準的な書式であれば、第2引数を指定する必要はありませんが、
今回は元データに合わせて「書式化コード」で指定しています。
使用できる書式化コードは、Pandasの公式サイトで確認できます。
Pandas公式サイトは、こちら
# 文字列にして、timeオブジェクトに変換
df_web['dateTime'] = pd.to_datetime(df_web.loc[:, '年月日時'].astype(str), format='%Y/%m/%d %H:%M')
# Pandasデータフレームを表示
display(df_web)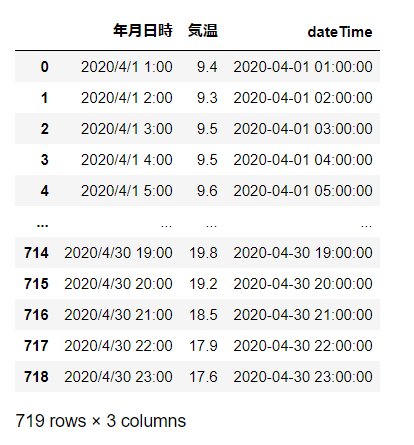
データフレーム「df_web」のデータ型を見てみましょう。
# データ型を表示
df_web.info()
列名「dateTime」は、datetime64型と確認できます。
年月日、時間、曜日を抽出
dtアクセサを使用して、時間の属性を取得します。
取得した値は、Pandasデータフレームに入れておきます。
# 時間の属性を取得
df_web.loc[:, 'Year'] = df_web.loc[:, 'dateTime'].dt.year
df_web.loc[:, 'Month'] = df_web.loc[:, 'dateTime'].dt.month
df_web.loc[:, 'Day'] = df_web.loc[:, 'dateTime'].dt.day
df_web.loc[:, 'Hour'] = df_web.loc[:, 'dateTime'].dt.hour
df_web.loc[:, 'Minute'] = df_web.loc[:, 'dateTime'].dt.minute
df_web.loc[:, 'Week'] = df_web.loc[:, 'dateTime'].dt.dayofweek
# Pandasデータフレームを表示
display(df_web)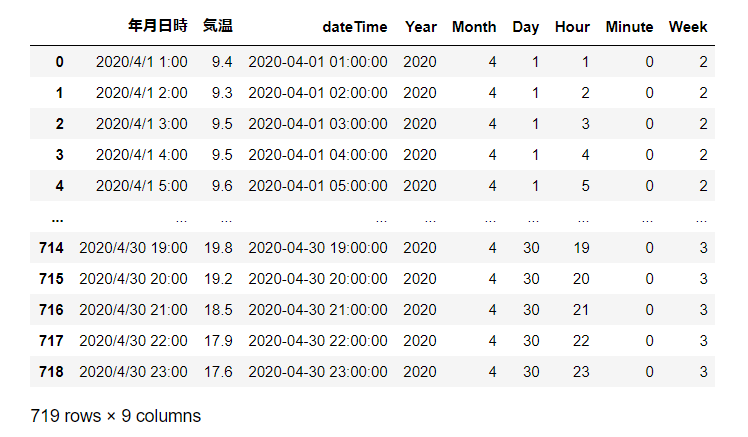
時刻を三角関数で、円状に配置
時刻は、周期性をもつ特徴量です。
円状に配置したときの位置を特徴量にして、周期性を表現してみます。
# 時刻を三角関数で、円状に配置
# 24時間を、0から1までの値に変換
clock24 = df_web.loc[:, 'Hour']/24 + df_web.loc[:, 'Minute']/60/100
# データフレームに入れる
df_web['clock24'] = clock24
# 三角関数で変換
df_web['sin'] = np.sin(2 * np.pi * clock24)
df_web['cos'] = np.cos(2 * np.pi * clock24)
# Pandasデータフレームを表示
display(df_web)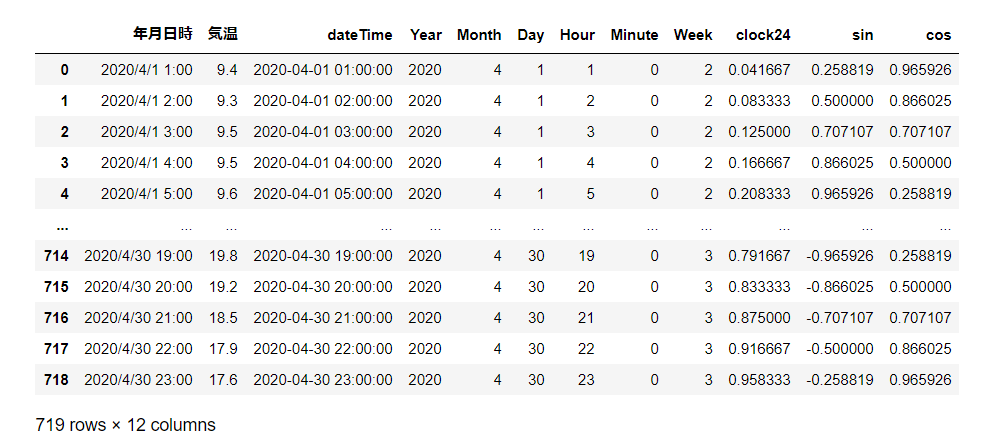
時刻がどのように表現されているのか、
円状に配置したときの位置になっているのか、
データの0行から24行までを、散布図にして見てみましょう。
# データフレームの列番号を取得
sin = df_web.columns.get_loc('sin')
cos = df_web.columns.get_loc('cos')
# グラフを表示
# 図の大きさを指定
plt.figure(figsize=(4, 4))
#(x, y) = (sin, cos)
plt.scatter(df_web.iloc[:24, sin], df_web.iloc[:24, cos])
# 1時をオレンジ色
plt.scatter(df_web.iloc[0, sin], df_web.iloc[0, cos], color='orange')
# 14時を赤色
plt.scatter(df_web.iloc[13, sin], df_web.iloc[13, cos], color='r')
# ラベルとタイトル
plt.xlabel('sin')
plt.ylabel('cos')
# 描画
plt.show()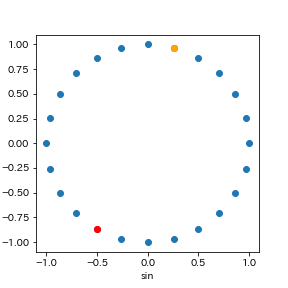
0時を頂点に、時計回り(右回り)に、24時間で1周しています。
黄色の点が、1時
赤色の点が、14時
時刻の近い、遠いの関係が、円状の配置で表現されています。
詳しくは、次の記事をご覧ください。
【Python覚書】周期性をもつ特徴量を(sin, cos)で円状に配置してみる
モデルの作成
特徴量の作成ができたので、気温を予測するモデルを2つ作成します。
・24時間の時刻を、そのまま使用するモデル
・時刻の特徴量を、円状に配置したモデル
24時間の時刻を、そのまま使用するモデル
データの抽出、分割
前処理をした気象データから、モデルの学習に使用するデータを抽出します。
1つ目のモデルは、「日付、時刻」が説明変数、「気温」が目的変数です。
# データの抽出
df_X = df_web[['Day', 'Hour']].copy()
y = df_web['気温'].values
4月1日から27日までのデータを、学習に使用し、
4月28日から30日までの気温を予測します。
# 4月1日から27日までを、学習データ
X_train = df_X.iloc[:647, :]
X_test = df_X.iloc[647:, :]
# 4月28日から30までを、テストデータ
y_train = y[:647]
y_test = y[647:]モデルの作成
scikit-learnを使って、線形モデルのリッジ回帰を行います。
リッジ回帰の説明は割愛しますが、コードの解説を簡単にします。
正則化の強弱は、alphaの値を[0.1, 1, 5, 10]の4種類で試しています。
ライブラリが、最も精度のよかったものを採用してくれます。
normalizeをTrueにして、説明変数を事前に正規化しています。
説明変数のスケールの違いが、モデルに影響しないようにするためです。
cv(交差検証)は、5回。
scoring(モデル評価)は、平均二乗誤差。
パラメーターの詳細は、scikit-learnの公式サイトで確認できます。
scikit-learnの公式サイトは、こちら
# リッジ回帰(交差検証5回)
ridge_modelCV = RidgeCV(
fit_intercept=True,
alphas=[0.1, 1, 5, 10],
normalize=True,
cv=5,
scoring='neg_mean_squared_error')
# 学習
ridge_modelCV.fit(X_train, y_train)
モデルで予測
作成したモデルで、4月28日から30日までの気温を予測します。
# 予測
y_preds = ridge_modelCV.predict(X_test)
# 平均平方二乗誤差
rmse_err = np.sqrt(np.mean(np.square(y_preds - y_test)))
print('RidgeCV model RMSE error:', rmse_err)
RMSE(平均平方二乗誤差率)は、0に近い方がよい値です。
1つ目のモデルのRMSE: 4.4645と、2つ目のモデルの結果を比較します。
4月26日以降、正答と予測値をグラフで比較してみましょう。
予測値は、4月28日以降の赤い点です。
グラフ用に、日付を取得
df_preds = df_web[['dateTime']].copy()
# 予測値を、4月28日以降の行へ入れる
df_preds['preds'] = 0
df_preds.iloc[647:, 1] = y_preds# データフレームの列番号を取得
sin = df_web.columns.get_loc('sin')
cos = df_web.columns.get_loc('cos')
dateTime = df_web.columns.get_loc('dateTime')
tmp = df_web.columns.get_loc('気温')
# グラフを表示
# 図の大きさを指定
plt.figure(figsize=(18, 4))
# 気温を追加
plt.scatter(df_web.iloc[600:, dateTime], df_web.iloc[600:, tmp], label='気温')
# 予測値を追加
plt.scatter(df_preds.iloc[647:, 0], df_preds.iloc[647:, 1], color='r', label='予測値')
# 凡例の表示
plt.legend()
# 描画
plt.show()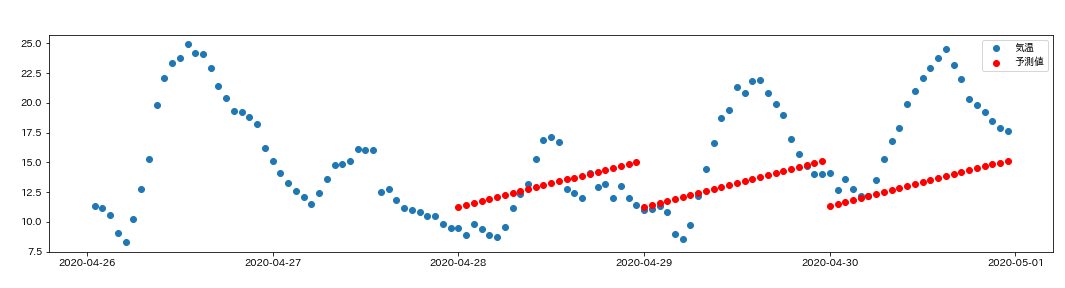
このモデルは、時刻の変化に伴う気温の変化をとらえられていないようです。
時刻の特徴量を、円状に配置したモデル
データの抽出、分割
前処理をした気象データから、モデルの学習に使用するデータを抽出します。
2つ目のモデルは、「日付、時刻(sin, cos)」が説明変数、「気温」が目的変数です。
# データの抽出
df_X = df_web[['Day', 'sin', 'cos']].copy()
y = df_web['気温'].values
分割は、1つ目のモデルと同じように、
4月1日から27日までのデータを、学習に使用し、
4月28日から30日までの気温を予測します。
# 4月1日から27日までを、学習データ
X_train = df_X.iloc[:647, :]
X_test = df_X.iloc[647:, :]
# 4月28日から30までを、テストデータ
y_train = y[:647]
y_test = y[647:]モデルの作成
モデルの作成も、1つ目のモデルと同じです。
# リッジ回帰(交差検証5回)
ridge_modelCV = RidgeCV(
fit_intercept=True,
alphas=[0.1, 1, 5, 10],
normalize=True,
cv=5,
scoring='neg_mean_squared_error')
# 学習
ridge_modelCV.fit(X_train, y_train)
モデルで予測
作成したモデルで、4月28日から30日までの気温を予測します。
# 予測
y_preds = ridge_modelCV.predict(X_test)
# 平均平方二乗誤差
rmse_err = np.sqrt(np.mean(np.square(y_preds - y_test)))
print('RidgeCV model RMSE error:', rmse_err)
RMSE(平均平方二乗誤差率)は、1つ目のモデルの4.4645 から改善しています。
4月26日以降、正答と予測値をグラフで比較してみましょう。
予測値は、4月28日以降の赤い点です。
1つ目のモデルと同じコードですが、
#グラフ用に、日付を取得
df_preds = df_web[['dateTime']].copy()
# 予測値を、4月28日以降の行へ入れる
df_preds['preds'] = 0
df_preds.iloc[647:, 1] = y_preds# データフレームの列番号を取得
sin = df_web.columns.get_loc('sin')
cos = df_web.columns.get_loc('cos')
dateTime = df_web.columns.get_loc('dateTime')
tmp = df_web.columns.get_loc('気温')
# グラフを表示
# 図の大きさを指定
plt.figure(figsize=(18, 4))
# 気温を追加
plt.scatter(df_web.iloc[600:, dateTime], df_web.iloc[600:, tmp], label='気温')
# 予測値を追加
plt.scatter(df_preds.iloc[647:, 0], df_preds.iloc[647:, 1], color='r', label='予測値')
# 凡例の表示
plt.legend()
# 描画
plt.show()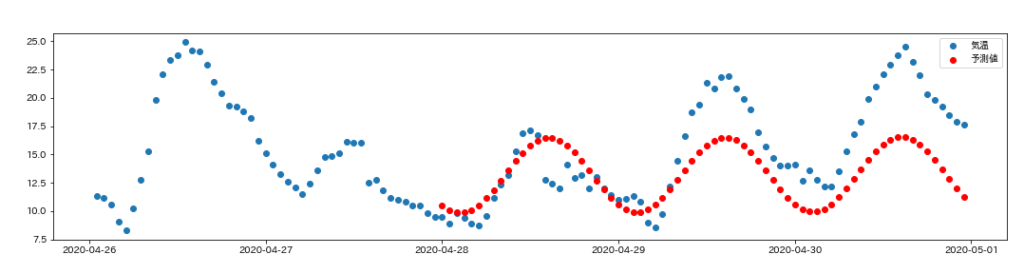
2つ目のモデルは、時刻の変化に伴う気温の変化をとらえているように見えます。
このモデルでは、時刻を円状に配置する前処理は効果があったと考えられます。
まとめ
線形モデルでは、時刻を円状に配置する前処理をすることで、時刻の特徴をつかむことができました。
時系列データの前処理として、試してみる価値があると思います。
本文では触れていませんが、時刻という1つの特徴量を、sinとcosの2つに分けることは、
メリットもありますが、デメリットもあります。
研究してみてください。

