時刻は、0時から12時まで続くと、0時に戻って1時へと続きます。
このような周期的な変動がある特徴量は、ひと工夫してからモデルに加えましょう。
周期性をもつ特徴量
12時間でひと回りするアナログ時計をイメージしてみます。
長針は0時から12時で一周します。
12時で頂点に戻ると、時刻は0時となるので、11時と0時は隣り合っています。
次に、デジタル時計をイメージしてみます。
0時から11時まで、数値として大きくなるので、11時と0時は最も離れています。
このように、時刻を数値として扱うことで、時刻の傾向を上手く学習できないことがあります。
周期的な変動がある特徴量は、円状に配置したときの位置で表現することで、その周期性を反映した特徴量にすることができます。
円状に特徴量を配置してみる
サンプルコード
12時間でひと回りするアナログ時計を作ってみます。
# 使用するライブラリ
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline# 空のデータフレームを作成
df_clock12 = pd.DataFrame()
# 0から11までのリストを作成
clock12 = list(range(12))
# データフレームに入れる
df_clock12['clock12'] = clock12
# sin, cosへの変換
df_clock12['sin'] = np.sin(2 * np.pi * df_clock12['clock12']/12)
df_clock12['cos'] = np.cos(2 * np.pi * df_clock12['clock12']/12)# グラフを表示
plt.scatter(df_clock12['sin'], df_clock12['cos'])
# ラベルとタイトル
plt.xlabel('sin')
plt.ylabel('cos')
plt.title('12時間時計')
# 描画
plt.show()
0から11までの数値を、円状に配置できました。
これで、頂点の0時と、左隣の11時は、隣り合うことが表現されています。
サンプルコードの解説
# 0から11までのリストを作成
clock12 = list(range(12))
# データフレームに入れる
df_clock12['clock12'] = clock12リスト「clock12」に、0から11までの数値を入れてから、データフレーム「df_clock12」に入れています。
これは、説明用に分けているだけです。
# sin, cosへの変換
df_clock12['sin'] = np.sin(2 * np.pi * df_clock12['clock12']/12)
df_clock12['cos'] = np.cos(2 * np.pi * df_clock12['clock12']/12)0から11までの数字を、三角関数で変換しています。
詳しくは、あとで解説します。
データフレームの中を見てみましょう。
display(df_clock12)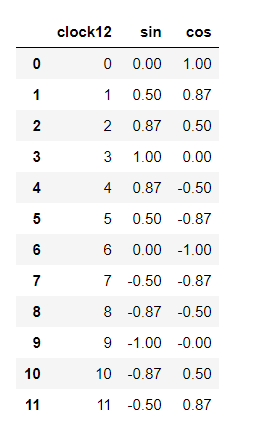
0から11までの、sinとcosです。
(x, y) = (sin, cos) として、散布図を描きます。
# グラフを表示
plt.scatter(df_clock12['sin'], df_clock12['cos'])0が頂点で、時計回り(右回り)に1から配置されます。
三角関数のポイントだけ
np.sin(x) と np.cos(x) で、三角関数を使っています。
パラメーター(x)に、何を入れるのか。
答えは、「角度」です。
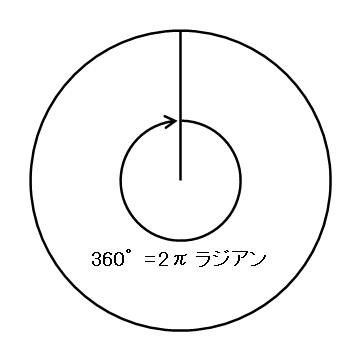
ただし、1周360°は、2π(パイ)ラジアンで表します。
例えば、時計の3時だと、角度は90°になります。
90° を 360°で割ると、1/4ですね。
ラジアンだと、2π に 1/4 を掛けた値になります。
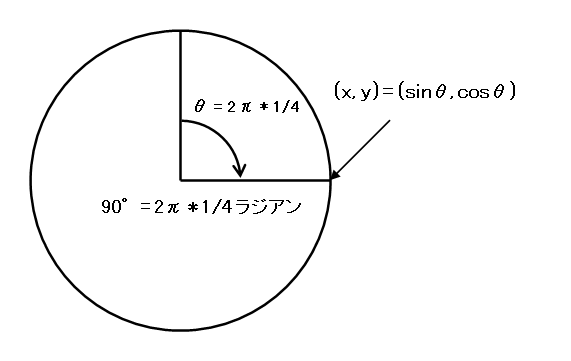
もう一度、コードを見てみましょう。
# sin, cosへの変換
df_clock12['sin'] = np.sin(2 * np.pi * df_clock12['clock12']/12)
df_clock12['cos'] = np.cos(2 * np.pi * df_clock12['clock12']/12)パラメータ(x)は、0から11までの数値を、12で割った値を、2πに掛けた値です。
x = 2π * [0/12, 1/12, 2/12, ・・・, 11/12]
このように、角度を分割することで、円状に配置することができます。
週だと「7」、年だと「12」で割ればよいです。
【参考】
時刻は、60分で1時間が進むので、少し補足です。
時刻(時分)は、24時間+60分で角度を分割します。
時間は、24で割り、分は、60で割って進法を合わせます。
また、0~1で時刻を表現するので、小数点以下1,2桁を時間、
小数点以下3,4桁を分、として加算します。
例)23時59分 → 23/24 + 59/60/100 = 0.96816
これを、2πに掛けて、角度にします。
θ = 2π * 0.968161
24時間で、1周します。
同じように、時刻(時分秒)は、24時間+60分+60秒で角度を分割します。
例)23時59分59秒 → 23/24 + 59/60/100 + 59/60/10000 = 0.968265
24時間でひと回りする時計を作る
それでは、24時間でひと回りする時計を作ってみましょう。
サンプルコード(12時間の時計)のどこを変更するのか、少し考えてみてください。
変更点は、2か所だけです。
では、24時間の時計のサンプルコードです。
変数名が12から24に変わっているのは、変更点のカウント外ですよ。
# 空のデータフレームを作成
df_clock24 = pd.DataFrame()
# 0から23までのリストを作成
clock24 = list(range(24))
# データフレームに入れる
df_clock24['clock24'] = clock24
# sin, cosへの変換
df_clock24['cos'] = np.cos(2 * np.pi * df_clock24['clock24']/24)
df_clock24['sin'] = np.sin(2 * np.pi * df_clock24['clock24']/24)# グラフを表示
plt.scatter(df_clock24['sin'], df_clock24['cos'])
# ラベルとタイトル
plt.xlabel('sin')
plt.ylabel('cos')
plt.title('24時間時計')
# 描画
plt.show()
変更点は、
・リストの値の数
・分割数
でした。
まとめ
周期性をもつ特徴量を(sin, cos)で円状に配置してみました。
1つの特徴量では表現できない周期性を、2つに分けることで表現しています。
ポイントの「角度の分割」だけ押さえれば、バッチリです。
どんな周期の特徴量でも変換できますよ。
モデルの作成で効果があるのか、試してみてください。
関連情報の記事では、線形モデルで使用しています。


