前回までの記事で、「分類」を目的として、LightGBMやXGBoostのモデルをトレーニングしてみました。
今回は、もう一つの「教師あり学習」の分野である「回帰分析」を、交差検証によるLightGBMのモデルで解いてみます。
課題の設定
住宅の価格を予測するデータセットを使用して、回帰モデルを作成します。
回帰モデルの目的変数は連続値をとるので、予測値との関係を可視化することで、モデルがデータセットの特徴量をどのくらい表現しているかわかります。
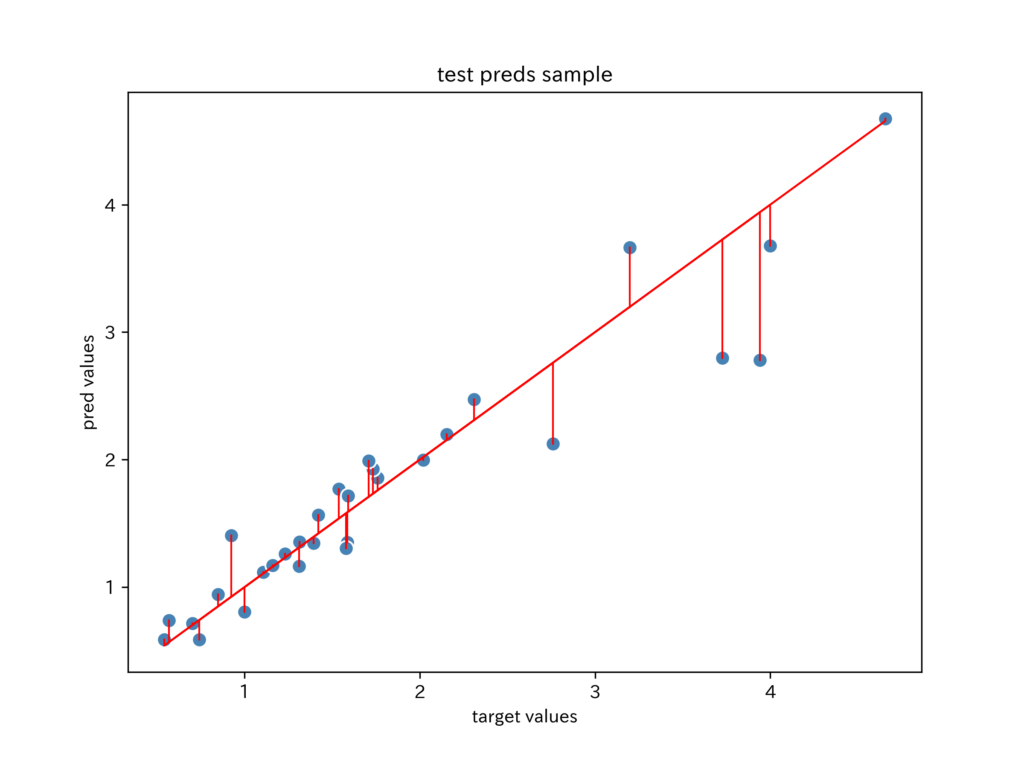
横軸を目的変数(正答値)、縦軸を予測値とした散布図を、青い点でプロットしています。
目的変数(正答値)を右上がりの赤い直線でプロットすると、青い点との距離でモデルの性能がわかります。
もちろん、距離が近いほど、正確な予測値です。
それでは、データセットの読込から学習過程の可視化まで、以下の作業をやってみます。
分析は、カリフォルニアの住宅価格データセットを使用します。
・scikit-learnの公式サイト
- データセットの読み込み
- 特徴量の確認
- モデルの作成
- モデルの評価
- 学習過程の可視化
- 予測値の可視化
使用するライブラリ
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import lightgbm as lgb
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_errorLightGBMは、インストールされている前提でインポートしています。
インストールガイドは、以下(英語)にあります。
・Installation Guide
なお、インストール方法は、先人のブログがたくさんありますので、自身のPC環境に合った方法を探してみてください。
データセット
# カリフォルニアの住宅価格データセットを読み込む
housing = datasets.fetch_california_housing()
X = housing['data']
y = housing['target']
# 説明変数をpandas.DataFrameに入れ、カラム名を付ける
df_X = pd.DataFrame(X, columns=housing['feature_names'])sklearn.datasetsからカリフォルニアの住宅価格データセットを読み込みます。
説明変数housing[‘data’]を変数X、目的変数housing[‘target’]を変数yに格納しています。
変数Xは、各要素(特徴量)の名称housing[‘feature_names’]をカラム名として、pandas.DataFrameに格納することで、pandasの強力なメソッドが使用できるようにします。
特徴量の確認
説明変数を確認します。
先頭の5行を取得します。
df_X.head()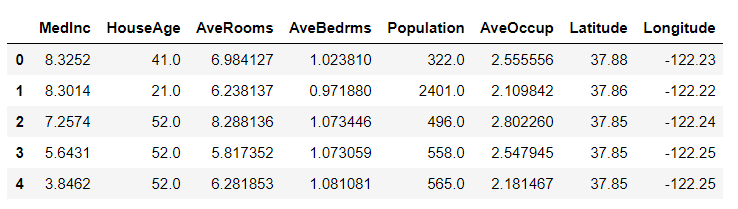
説明変数は、8個の加工されていないデータです。
LightGBMは、トレーニングデータセットの特徴量を標準化する必要がないので、そのまま使用します。
交差検証
交差検証をする理由
「分類」のモデルでは、交差検証は高い効果があったので、回帰分析でも取り入れたいと思います。
詳しい解説は、以下の記事をご覧ください。
【Python覚書】LightGBMで交差検証を実装してみる
今回、交差検証を行う一番の理由は、トレーニングデータ全体の予測値を得るためです。
5分割交差検証では、5回分の予測値をまとめると、トレーニングデータ全体の予測値になります。
このデータで上記のような散布図を描くことで、モデルの性能を可視化することができます。
もちろん、5個のモデルで予測することで、汎化性能を高める効果も期待しています。
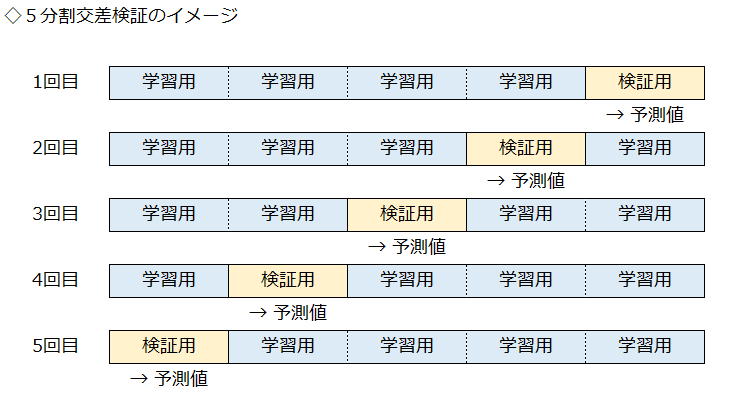
LightGBMでアーリーストッピングを使用する場合
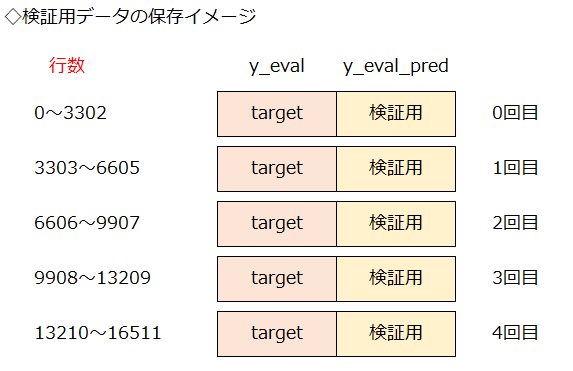
LightGBMでアーリーストッピングを使用する場合は、下図の中段のように、検証用データがハイパーパラメータの調整に使用されます。
そのため、モデルは学習時に、本来は見ないことになっている検証用データを見てしまいます。
学習には使用されませんが、検証用データでの性能評価で、学習の進み具合を観察します。
アーリーストッピングでは、検証用データでの性能評価で、最もよい値のハイパーパラメータが採用されます。
通常の交差検証では、検証用データは、完全に分離されているので、検証用データでの予測値の精度は信用できます。
アーリーストッピングを使用したLightGBMでは、検証用データでの予測値の精度が過度に高くなる場合もあるので、更に確認をしておいた方が無難です。
学習に使用できるデータ少なくなるデメリットがありますが、予測値の精度を確認するため、上段の図のように、完全に分離したテストデータでモデルを評価します。

データの分割
説明変数のデータを、学習データとテストデータに分けます。
# 学習データとテストデータに分ける
X_train, X_test, y_train, y_test = train_test_split(df_X, y,
test_size=0.2,
random_state=0)モデルの作成
コード全文
交差検証は、for文を使って実装しています。
インデントがズレると、コードが実行できないので、一括して掲載します。
解説は、コメントで記したブロック毎に行います。
# 5-fold CVモデルの学習
# 【ブロック1: 初期化】
# 5つのモデルを保存するリストの初期化
models = []
# 学習用データでの予測値を保存するデータフレームの初期化
df_train_preds = pd.DataFrame({'y_train': y_train})
# 検証用データでの予測値を保存するデータフレームの初期化
df_eval_preds = pd.DataFrame({'y_eval': [],
'y_eval_pred': []})
# テストデータでの予測値を保存するデータフレームの初期化
df_test_preds = pd.DataFrame({'y_test': y_test})
# インデックスが0からの連番になるように初期化
df_test_preds.reset_index(inplace=True, drop=True)
# R^2を保存するデータフレームの初期化
df_R2 = pd.DataFrame({'train': [],
'eval': [],
'test': []})
# RMSEを保存するデータフレームの初期化
df_RMSE =pd.DataFrame({'train': [],
'eval': [],
'test': []})
# ラウンド数の初期化
round_no = 0
# 【ブロック2: モデルの学習】
# 学習データの数だけの数列(0行から最終行まで連番)
row_no_list = list(range(len(y_train)))
# KFoldクラスをインスタンス化(これを使って5分割する)
K_fold = KFold(n_splits=5, shuffle=True, random_state=42)
# KFoldクラスで分割した回数だけ実行(ここでは5回)
for train_cv_no, eval_cv_no in K_fold.split(row_no_list, y_train):
# ilocで取り出す行を指定
X_train_cv = X_train.iloc[train_cv_no, :]
y_train_cv = pd.Series(y_train).iloc[train_cv_no]
X_eval_cv = X_train.iloc[eval_cv_no, :]
y_eval_cv = pd.Series(y_train).iloc[eval_cv_no]
# 学習用
lgb_train = lgb.Dataset(X_train_cv, y_train_cv,
free_raw_data=False)
# 検証用
lgb_eval = lgb.Dataset(X_eval_cv, y_eval_cv, reference=lgb_train,
free_raw_data=False)
# パラメータを設定
params = {'task': 'train', # 学習、トレーニング ⇔ 予測predict
'boosting_type': 'gbdt', # 勾配ブースティング
'objective': 'regression', # 目的関数:回帰
'metric': 'rmse', # 分類モデルの性能を測る指標
'learning_rate': 0.1 } # 学習率(初期値0.1)
# 学習
evaluation_results = {} # 学習の経過を保存する箱
model = lgb.train(params, # 上記で設定したパラメータ
lgb_train, # 使用するデータセット
num_boost_round=1000, # 学習の回数
valid_names=['train', 'valid'], # 学習経過で表示する名称
valid_sets=[lgb_train, lgb_eval], # モデル検証のデータセット
evals_result=evaluation_results, # 学習の経過を保存
early_stopping_rounds=20, # アーリーストッピング
verbose_eval=0) # 学習の経過の非表示
# 学習が終わったモデルをリストに保存
models.append(model)
# 【ブロック3: モデルで予測】
# 学習したモデルで予測
y_train_pred = model.predict(X_train_cv, num_iteration=model.best_iteration)
y_eval_pred = model.predict(X_eval_cv, num_iteration=model.best_iteration)
y_test_pred = model.predict(X_test, num_iteration=model.best_iteration)
# 学習用データでの予測値をデータフレームに保存
df_train_cv_pred = pd.DataFrame({round_no: y_train_pred},
index=train_cv_no)
df_train_preds = df_train_preds.join(df_train_cv_pred, how='left')
# 検証用データでの予測値をデータフレームに保存
df_eval_pred = pd.DataFrame({'y_eval': y_eval_cv,
'y_eval_pred': y_eval_pred})
df_eval_preds = df_eval_preds.append(df_eval_pred)
# テストデータでの予測値をデータフレームに保存
df_test_cv_pred = pd.DataFrame({round_no: y_test_pred})
df_test_preds = pd.concat([df_test_preds, df_test_cv_pred], axis=1)
# r2_score を計算
train_score = r2_score(y_train_cv, y_train_pred)
eval_score = r2_score(y_eval_cv, y_eval_pred)
test_score = r2_score(y_test, y_test_pred)
# RMSE を計算
train_RMSE_score = np.sqrt(mean_squared_error(y_train_cv, y_train_pred))
eval_RMSE_score = np.sqrt(mean_squared_error(y_eval_cv, y_eval_pred))
test_RMSE_score = np.sqrt(mean_squared_error(y_test, y_test_pred))
# スコアを表示
print('R^2 train: %.5f, eval: %.5f, test: %.5f'
% (train_score, eval_score, test_score),
' | RMSE train: %.5f, eval: %.5f, test: %.5f'
% (train_RMSE_score, eval_RMSE_score, test_RMSE_score))
# R2の保存
df_R2_cv = pd.DataFrame({'train': [train_score],
'eval': [eval_score],
'test': [test_score]},
index=[round_no])
df_R2 = df_R2.append(df_R2_cv)
# RMSEの保存
df_RMSE_cv =pd.DataFrame({'train': [train_RMSE_score],
'eval': [eval_RMSE_score],
'test': [test_RMSE_score]},
index=[round_no])
df_RMSE = df_RMSE.append(df_RMSE_cv)
# ラウンド数のカウンタを更新
round_no += 1
# 保存したR2の平均値
R2_ave = df_R2.mean().to_numpy()
# 保存したRMSEの平均値
RMSE_ave = df_RMSE.mean().to_numpy()
# 平均値を表示
print('Average:')
print('R^2 train: %.5f, eval: %.5f, test: %.5f'
% (R2_ave[0], R2_ave[1], R2_ave[2]),
' | RMSE train: %.5f, eval: %.5f, test: %.5f'
% (RMSE_ave[0], RMSE_ave[1], RMSE_ave[2]))ブロック1: 初期化
実行結果を保存するために、リストやデータフレームで空箱を作っています。
データフレームは、カラム名を決め、必要な列数を確保します。
交差検証のラウンド数は、round_noで管理します。
0回目が終わると、カウンターに1加算します。
# ラウンド数の初期化
round_no = 0# ラウンド数のカウンタを更新
round_no += 1ブロック2: モデルの学習
5分割交差検証
5分割交差検証を行うので、5通りの分割を行い、5回の学習と検証を行うことで、5個のモデルを作ります。
モデルの分割は、以下の手順で行います。
- 学習データの数だけの数列(0行から最終行まで連番)を作成
- KFoldクラスをインスタンス化(これを使って5分割する)
- KFoldクラスで分割した回数だけ実行(ここでは5回)
# KFoldクラスで分割した回数だけ実行(ここでは5回)
for train_cv_no, eval_cv_no in K_fold.split(row_no_list, y_train):
# ilocで取り出す行を指定
X_train_cv = X_train.iloc[train_cv_no, :]
y_train_cv = pd.Series(y_train).iloc[train_cv_no]
X_eval_cv = X_train.iloc[eval_cv_no, :]
y_eval_cv = pd.Series(y_train).iloc[eval_cv_no]for文で、KFoldクラスが連番の数列(row_no_list)を、学習用(train_cv_no)と検証用(eval_cv_no)に分割するので、その番号と同じインデックスの行を指定(iloc)して抽出します。
これは、「X_train」のインデックスが重複のない連番であることを利用しています。
numpy配列の「y_train」はインデックが利用できないため、pandas.Seriesに変換してから、インデックスを利用しています。
LightGBMのモデル
# パラメータを設定
params = {'task': 'train', # 学習、トレーニング ⇔ 予測predict
'boosting_type': 'gbdt', # 勾配ブースティング
'objective': 'regression', # 目的関数:回帰
'metric': 'rmse', # 回帰分析モデルの性能を測る指標
'learning_rate': 0.1 } # 学習率(初期値0.1)パラメータは初期値のままで、回帰分析のモデルを作成します。
回帰分析を行うので、objectiveに「regression」を設定します。
評価関数metricは、「rmse」を使用します。
パラメータの詳細は、以下で確認ください。
・LightGBMの公式サイト
ブロック3: モデルで予測
学習したモデルで予測
# 学習したモデルで予測
y_train_pred = model.predict(X_train_cv, num_iteration=model.best_iteration)
y_eval_pred = model.predict(X_eval_cv, num_iteration=model.best_iteration)
y_test_pred = model.predict(X_test, num_iteration=model.best_iteration)学習用データ、検証用データ、テストデータについて、学習済みのモデルで予測を行います。
引数(num_iteration)に、「model.best_iteration」を設定することで、アーリーストッピングで最も性能評価がよかったハイパーパラメータが使用されます。
予測値の保存
モデルの予測値は、2ステップで保存します。
1.仮置き用のデータフレームに入れる。
2.予め初期化しておいたデータフレームに追加(結合)する。
学習用データ、検証用データ、テストデータは、それぞれデータの形が違うので、別の方法を使用しています。
学習用データでの予測値
# 学習用データでの予測値をデータフレームに保存
df_train_cv_pred = pd.DataFrame({round_no: y_train_pred},
index=train_cv_no)
df_train_preds = df_train_preds.join(df_train_cv_pred, how='left')
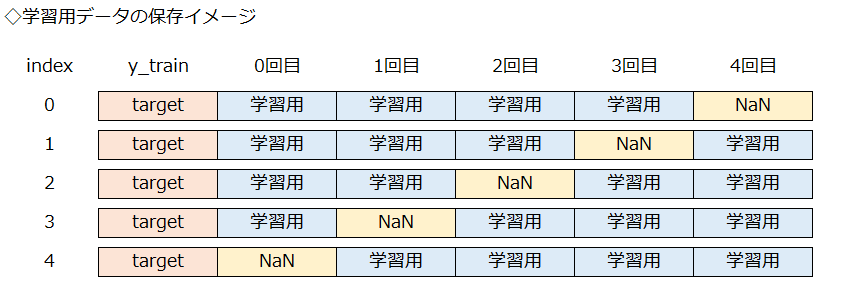
学習用データは、交差検証の各ラウンドでランダムに選択されます。
0から4回目までの5ラウンドで、学習用データとして4回使用されます。
学習用データでの予測値を保存するデータフレームは、初期化で列名「y_train」に目的変数(target)を入れており、indexは0からの連番になっています。
仮置き用のデータフレームには、検証用と分割する前の「index」を指定して入れます。
そうすることで、indexが同じ値の「y_train」と「予測値」を横に並べて結合することができます。
注意する点として、indexは〇行目を指す値ではなく、各行ごとに付けられた「行の名前」です。
重複しない「行の名前」を使って、目的変数と予測値を結びつけています。
データフレームの結合に使用しているのは、pandas.DataFrameのjoinメソッドです。
引数を「how=’left’」に設定することで、結合する左側のデータフレームは全て残し、右側に同じindexのデータが結合されます。
各ラウンドで、検証用に使用した行(index)の予測値はないので、その行は「NaN」となります。
実際のデータは、以下のようになります。
display(df_train_preds)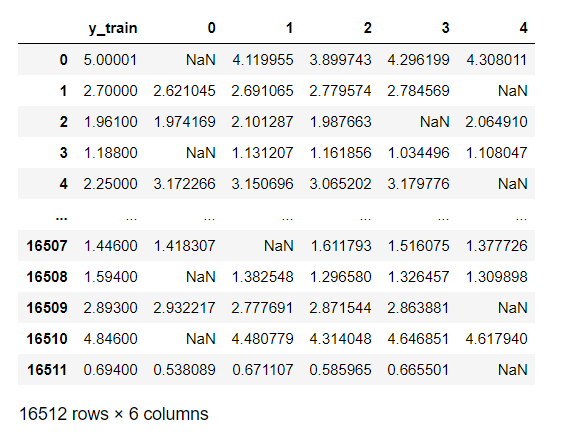
検証用データでの予測値
# 検証用データでの予測値をデータフレームに保存
df_eval_pred = pd.DataFrame({'y_eval': y_eval_cv,
'y_eval_pred': y_eval_pred})
df_eval_preds = df_eval_preds.append(df_eval_pred)
検証用データも、交差検証の各ラウンドでランダムに選択されます。
学習用データとの違いは、0から4回目までの5ラウンドで、1回だけ使用されることです。
そのため、ラウンド毎に同じindexで結合した列を追加する必要はなく、行を追加していくだけでよいです。
データフレームへの追加に使用しているのは、pandas.DataFrameのappendメソッドです。
仮置き用のデータフレームに、検証用の目的変数(target)と予測値を入れ、データフレームの末尾に追加しています。
なお、「index」は明示的に設定していませんが、検証用と分割する前の「index」になっています。
実際のデータは、以下のようになります。
display(df_eval_preds)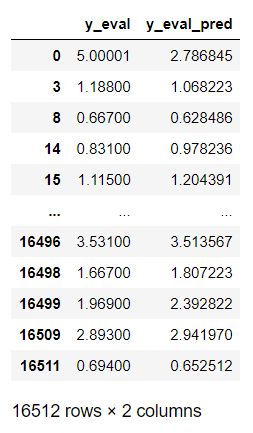
「index」は不連続ですが、行数は学習用データと同じ16512行です。
テストデータでの予測値
# テストデータでの予測値をデータフレームに保存
df_test_cv_pred = pd.DataFrame({round_no: y_test_pred})
df_test_preds = pd.concat([df_test_preds, df_test_cv_pred], axis=1)

テストデータは、交差検証の各ラウンドで「同じデータ」が使用されます。
0から4回目までの5ラウンドで、5回使用されますが、学習用データと違って、データの順番がまったく同じです。
そのため、indexを使って行ごとに結合する必要はなく、一塊の列として横に追加していきます。
joinメソッドで結合するよりは、concat()関数を使った処理の方が軽いです。
実際のデータは、以下のようになります。
display(df_test_preds)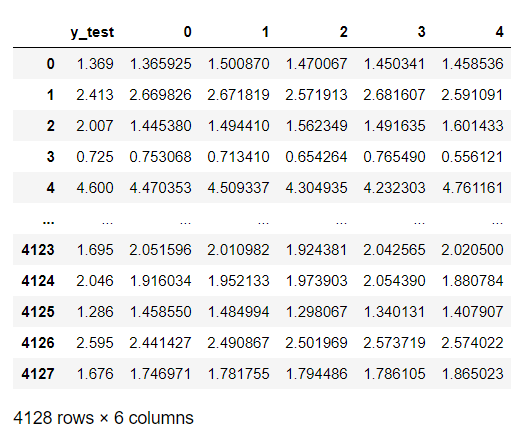
評価指標の計算
決定係数(R^2)を計算
# r2_score を計算
train_score = r2_score(y_train_cv, y_train_pred)
eval_score = r2_score(y_eval_cv, y_eval_pred)
test_score = r2_score(y_test, y_test_pred)scikit-learnのr2_score()関数を使用して、決定係数を計算します。
決定係数は、回帰モデルの評価指標で、0から1までの値を取り、1に近づくほど良い値です。
実際は、決定係数の値だけでモデルの評価は行うわけではなく、学習用・検証用・テストデータでの値を比較するなど、総合的にモデルを評価します。
二乗平均平方根誤差 (RMSE: Root Mean Squared Error )を計算
# RMSE を計算
train_RMSE_score = np.sqrt(mean_squared_error(y_train_cv, y_train_pred))
eval_RMSE_score = np.sqrt(mean_squared_error(y_eval_cv, y_eval_pred))
test_RMSE_score = np.sqrt(mean_squared_error(y_test, y_test_pred))scikit-learnのmean_squared_error()関数を使用して、平均二乗誤差(MSE)を計算します。
そのあとで、numpyのsqrt()関数を使用して、MSEの平方根(Root)を計算しています。
これは、scikit-learnにRMSEが実装されていないための処理です。
RMSEは、誤差の大きさを表す評価指標なので、0に近づくほど良い値です。
評価指標の保存
# R2の保存
df_R2_cv = pd.DataFrame({'train': [train_score],
'eval': [eval_score],
'test': [test_score]},
index=[round_no])
df_R2 = df_R2.append(df_R2_cv)
# RMSEの保存
df_RMSE_cv =pd.DataFrame({'train': [train_RMSE_score],
'eval': [eval_RMSE_score],
'test': [test_RMSE_score]},
index=[round_no])
df_RMSE = df_RMSE.append(df_RMSE_cv)計算した評価指標を、モデルの予測値と同じように、2ステップで保存します。
仮置き用のデータフレームに入れるときに、ラウンド数を「index」に設定しています。
実際のデータは、以下のようになります。
display(df_R2)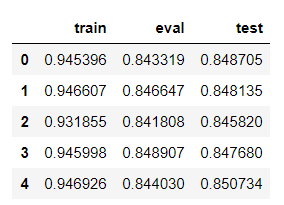
評価指標の表示
# スコアを表示
print('R^2 train: %.5f, eval: %.5f, test: %.5f'
% (train_score, eval_score, test_score),
' | RMSE train: %.5f, eval: %.5f, test: %.5f'
% (train_RMSE_score, eval_RMSE_score, test_RMSE_score))# 保存したR2の平均値
R2_ave = df_R2.mean().to_numpy()
# 保存したRMSEの平均値
RMSE_ave = df_RMSE.mean().to_numpy()
# 平均値を表示
print('Average:')
print('R^2 train: %.5f, eval: %.5f, test: %.5f'
% (R2_ave[0], R2_ave[1], R2_ave[2]),
' | RMSE train: %.5f, eval: %.5f, test: %.5f'
% (RMSE_ave[0], RMSE_ave[1], RMSE_ave[2]))
最後に、コードの出力部です。
出力は、上段のラウンド毎の結果と、Average以下の集計値に分かれます。
上段のラウンド毎の結果は、print()関数内のシングルコーテーション(’ ‘)で挟まれた文字列に、「%」以降の変数を差し込んでいます。
「%.5f」で、%に値を差し込み、小数点以下5桁を指定しています。
シングルコーテーション(’ ‘)内に、3個の%があるので、「%」以降の変数も丸括弧内に3個の値を用意する必要があります。
下段の集計値の出力では、縦方向に平均値を取ってから、numpy配列として値を取り出しています。
別の変数に代入するのは、print()関数中のコードを短くするためです。
# 保存したR2の平均値
R2_ave = df_R2.mean().to_numpy()式を分解していくと、まずは縦方向に平均値を取ります。
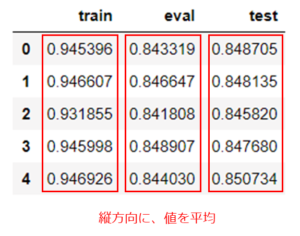
df_R2.mean()
meanメソッドで平均値を取ると、pandas.Seriesとして値が取得できます。
軸の指定は省略しており、初期値の「axis=0」で縦方向。
横方向にするときは、「axis=1」です。
次に、to_numpy()メソッドでnumpy配列にします。
df_R2.mean().to_numpy()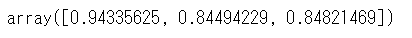
出力するときは、numpy配列のインデックスを指定します。
なお、pandasの「iat」プロパティや「iloc」メソッドを使っても同じことができます。
df_R2.mean().to_numpy()[0] # numpy.ndarray メソッドの使用
df_R2.mean().values[0] # numpy.ndarray values属性
df_R2.mean().iat[0] # pandas.Series 単独の要素のみ
df_R2.mean().iloc[0] # pandas.Series 複数の要素も可
df_R2.mean()[0] # pandas.Series 単独の要素(インデックス)
df_R2.mean()['train'] # pandas.Series 単独の要素(ラベル名)上からおすすめ順にしていますが、どの方法でも同じ値を取得できます。
明示的に指定しておくと、コードの可読性が高くなると思います。
モデルの評価
学習過程の可視化

モデルからの出力を確認します。
R^2は、1に近いほど良く、RMSEは、0に近いほど良い値です。
各ラウンドで大きな違いはないので、平均値で、「学習用」と、「検証用、テスト」を比較します。
「学習用」と、「検証用、テスト」に大きな差があると、過学習が疑われます。
このモデルはアーリーストッピングを使用しているので、大丈夫そうですが、学習過程を見てみます。
# 学習過程の可視化
plt.plot(evaluation_results['train']['rmse'], label='train')
plt.plot(evaluation_results['valid']['rmse'], label='valid')
plt.ylabel('RMSE')
plt.xlabel('Boosting round')
plt.title('Training performance')
plt.legend()
plt.show()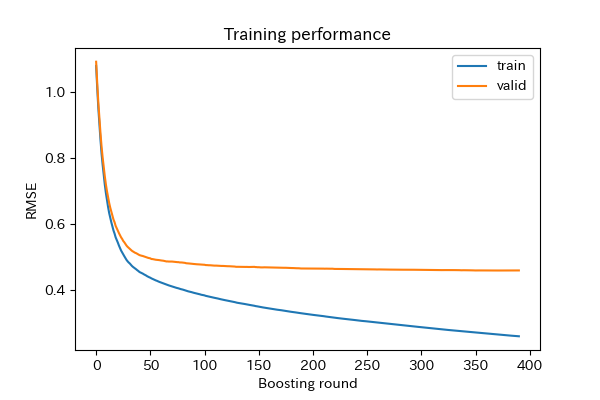
最後のラウンドの学習の経過が保存されているので、グラフにして確認します。
検証用(valid)は、50回位から値に変化はなく、学習用(train)との乖離が進んでいます。
アーリーストッピングするまでの回数を減らしてもいいのかもしれません。
「検証用」と「テスト」は、ほぼ同じ値です。
「検証用」をハイパーパラメータの調整に使った影響はないようです。
モデルのアンサンブル
交差検証で、5個のモデルを作成しました。
5個のモデルをアンサンブルすることで、精度の向上を図ります。
保存した予測値を使用
5個のモデルの予測値を学習時に保存しています。
このデータをアンサンブルします。
まず、データの構造を見てみます。
display(df_train_preds)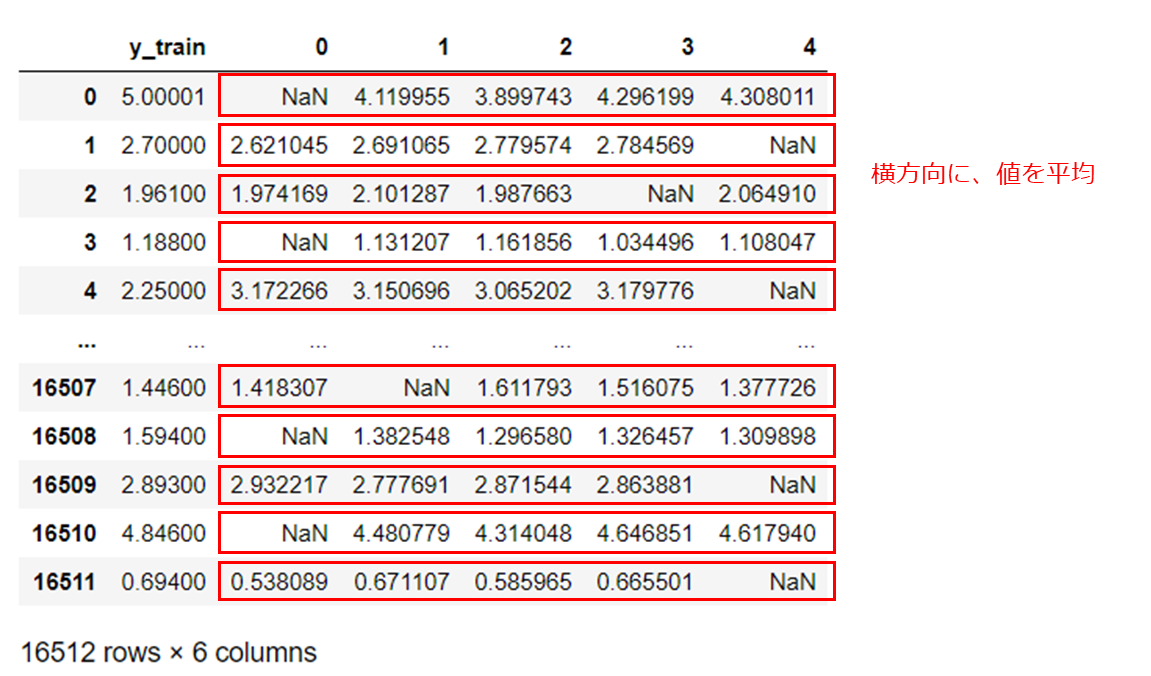
カラム名「0」から「4」に、各モデルでの予測値が入っています。
これを、横方向(行ごと)に、値の平均値を取ることで、5つのモデルをアンサンブルします。
# 保存した学習用、テストデータでの予測値を平均
train_preds_ave = df_train_preds.iloc[:, 1:].mean(axis=1).to_numpy()
test_preds_ave = df_test_preds.iloc[:, 1:].mean(axis=1).to_numpy()
# r2_score を計算
train_preds_ave_R2_score = r2_score(y_train, train_preds_ave)
test_preds_ave_R2_score = r2_score(y_test, test_preds_ave)
# RMSE を計算
train_preds_ave_RMSE_score = np.sqrt(mean_squared_error(y_train, train_preds_ave))
test_preds_ave_RMSE_score = np.sqrt(mean_squared_error(y_test, test_preds_ave))
# スコアを表示
print('R^2 train: %.5f, test: %.5f' % (train_preds_ave_R2_score, test_preds_ave_R2_score),
' | RMSE train: %.5f, test: %.5f' % (train_preds_ave_RMSE_score, test_preds_ave_RMSE_score))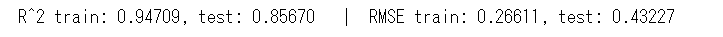
5ラウンドの平均値と比較すると、以下のとおり値が改善しました。
| R^2 train | test | RMSE train | test | |
| アンサンブル | 0.94709 | 0.85670 | 0.26611 | 0.43227 |
| 5ラウンド平均値 | 0.94336 | 0.84821 | 0.27499 | 0.44488 |
保存したモデルを使用
保存したモデルを使用して、学習後に予測値を求める方法です。
今回の交差検証では、学習済みのモデルが5個あります。
モデルは、リストに入れてあるので、1個ずつ取り出して予測値を求めます。
テストデータの予測値を、保存してあるモデルを使って、再度、計算してみます。
enumerate()関数は、ラウンドごとに連続値が得られるので、カラム名に使用しています。
# 予測値を保存するデータフレームの初期化
df_preds = pd.DataFrame()
# 保存してあるモデルで予測
for i, model in enumerate(models):
y_pred = model.predict(X_test, num_iteration=model.best_iteration)
df_preds[i] = y_pred
# 保存した予測値を表示
df_preds.head() 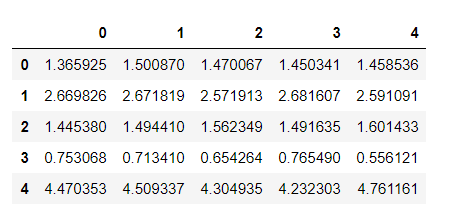
カラム名「0」から「4」に、各モデルでの予測値が入っています。
先ほどとの違いは、カラム名「y_train」がないことです。
予測値の平均値を取るときに、列番号をすべて指定しています。
# 保存した学習用データでの予測値の平均値
model_test_preds_ave = df_preds.iloc[:, :].mean(axis=1).to_numpy()
# r2_score を計算
model_test_preds_ave_R2_score = r2_score(y_test, model_test_preds_ave)
# RMSE を計算
model_test_preds_ave_RMSE_score = np.sqrt(mean_squared_error(y_test, model_test_preds_ave))
# スコアを表示
print('R^2 train: %.5f, test: %.5f' % (train_preds_ave_R2_score, model_test_preds_ave_R2_score),
' | RMSE train: %.5f, test: %.5f' % (train_preds_ave_RMSE_score, model_test_preds_ave_RMSE_score))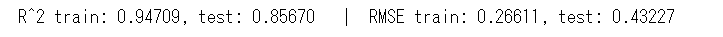
保存した予測値でのスコアと同じ結果になりました。
予測値の可視化
モデルの予測値が、目的変数に適合できているのか、可視化してみます。
縦軸を予測値、横軸を目的変数として散布図をプロットします。
散布図の見方
記事の冒頭に示した散布図を描きます。
# plot_data_sample関数を定義
def plot_data_sample(plt_target, plt_pred, plt_title):
# 描画サイズ
plt.figure(figsize=(8, 6))
# 目的変数と予測値の散布図
plt.scatter(plt_target, plt_pred, c='steelblue', edgecolor='white', s=70)
# 目的変数の直線
plt.plot(plt_target, plt_target, color='red', lw=1)
# ラベルとタイトル
plt.xlabel('target values')
plt.ylabel('pred values')
plt.title(plt_title)
# 補助線を追加
for i in list(range(20, 50)):
plt.plot([plt_target[i], plt_target[i]], [plt_target[i], plt_pred[i]], color='red', lw=1)
#plt.savefig('sample.png', dpi=300)
plt.show()# テストデータでの予測
# plot_data_sample関数へ送るデータ
plt_target = df_test_preds.iloc[20:50, 0]
plt_pred = df_test_preds.iloc[20:50, 1:].mean(axis=1)
plt_title = 'test preds sample'
# plot_data_sample関数でグラフを描画
plot_data_sample(plt_target, plt_pred, plt_title)
plot_data_sample関数を定義し、テストデータの一部を使って描画しています。
目的変数(正答値)が右上がりの赤い直線なので、予測値の青い点との距離が、誤差の大きさとなります。
青い点が赤い直線上の近くに密集しているのが望ましいです。
学習用データの予測値
まず、散布図を描画するplot_data関数を定義します。
# plot_data関数を定義
def plot_data(plt_target, plt_pred, plt_title, plt_R2, plt_RMSE):
# 描画サイズ
plt.figure(figsize=(8, 6))
# 目的変数と予測値の散布図
plt.scatter(plt_target, plt_pred, c='steelblue', edgecolor='white', s=70)
# 目的変数の直線
plt.plot(plt_target, plt_target, color='red', lw=2)
# ラベルとタイトル
plt.xlabel('target values')
plt.ylabel('pred values')
plt.title(plt_title)
# スコア
plt.text(0.1, 5.0, 'R^2: %.5f' % (plt_R2), fontsize=12)
plt.text(0.1, 4.7, 'RMSE: %.5f' % (plt_RMSE), fontsize=12)
plt.show()
学習用データでの予測値の散布図を描きます。
使用する予測値は、「モデルのアンサンブル」で作成した予測値の平均値です。
# 学習データでの予測
# plot_data関数へ送るデータ
plt_target = y_train
plt_pred = df_train_preds.iloc[:, :].mean(axis=1)
plt_title = 'train preds'
plt_R2 = train_preds_ave_R2_score
plt_RMSE = train_preds_ave_RMSE_score
# plot_data関数でグラフを描画
plot_data(plt_target, plt_pred, plt_title, plt_R2, plt_RMSE)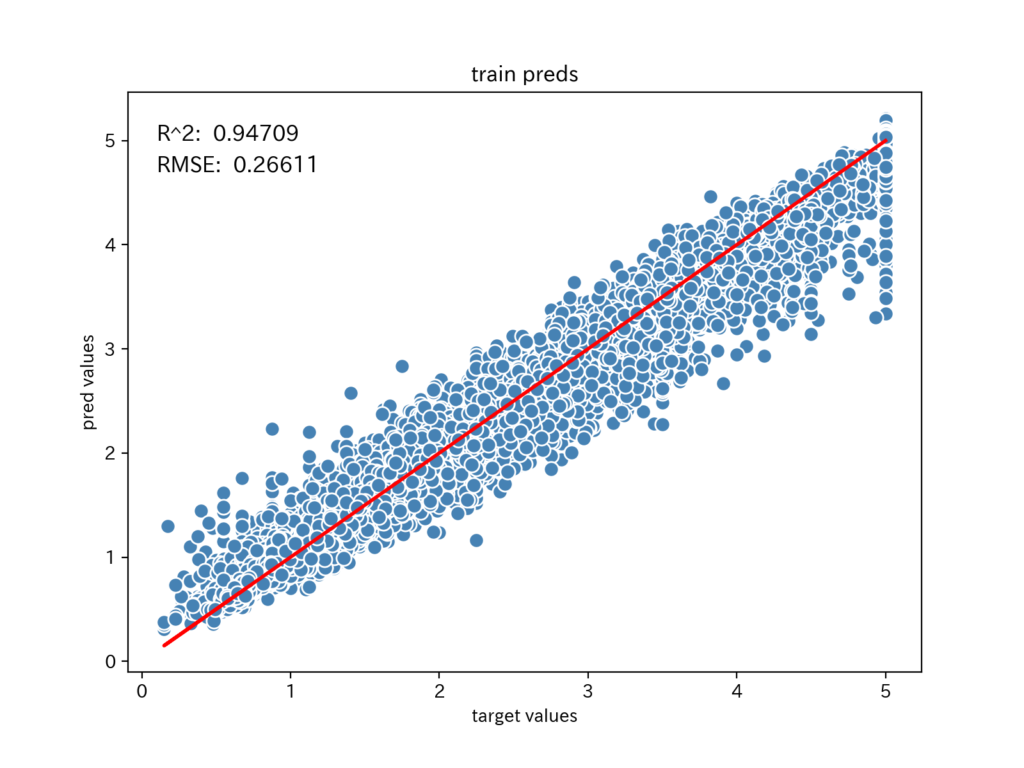
予測値は、赤い直線に沿っているように見えます。
誤差の分布を見てみると、目的変数が小さいときは、大きく予測しており、目的変数が大きくなるにつれて、小さく予測する傾向があるようです。
説明変数の特徴量エンジニアリングのヒントになりそうです。
検証用データの予測値
検証用データでの予測値の散布図を描きます。
使用する予測値は、交差検証で5個のモデルで、部分ごとに予測した値です。
学習用データのようにアンサンブルしたものではないので、個別のモデルでの予測性能がわかります。
# テストデータでの予測
# plot_data関数へ送るデータ
plt_target = df_test_preds.iloc[:, 0]
plt_pred = df_test_preds.iloc[:, 1:].mean(axis=1)
plt_title = 'test preds'
plt_R2 = test_preds_ave_R2_score
plt_RMSE = test_preds_ave_RMSE_score
# plot_data関数でグラフを描画
plot_data(plt_target, plt_pred, plt_title, plt_R2, plt_RMSE)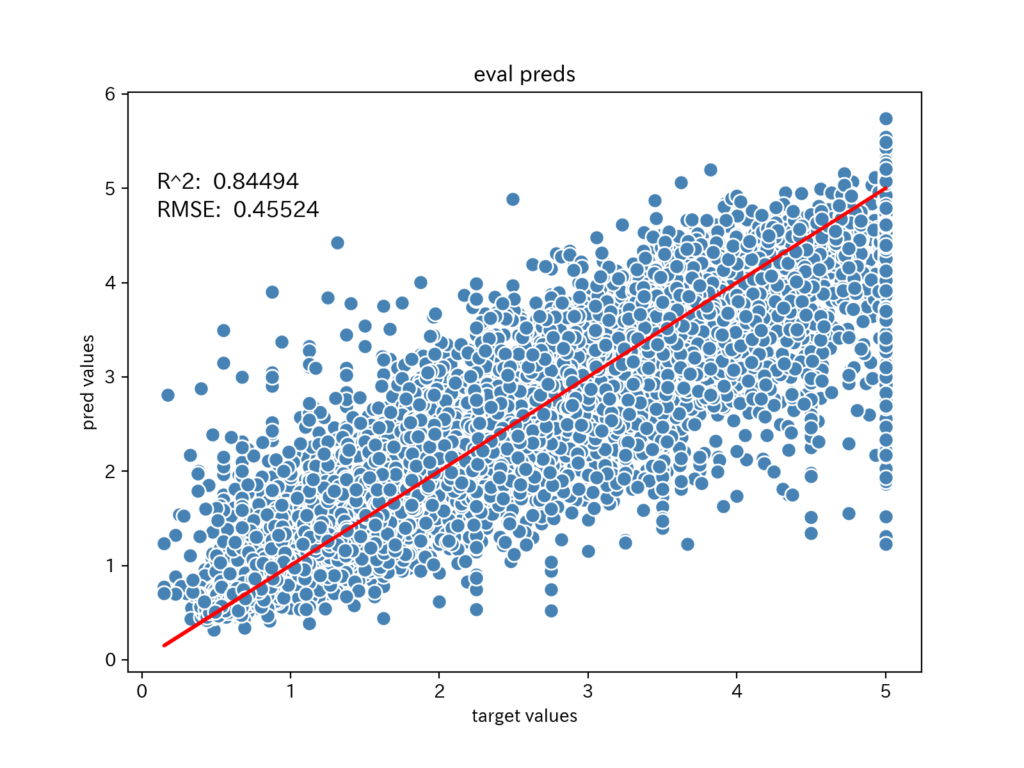
予測値は、赤い直線に沿っているものの、誤差が大きくなっていることがわかります。
誤差の分布は、学習データと同じ傾向があるようです。
テストデータの予測値
テストデータでの予測値の散布図を描きます。
使用する予測値は、「モデルのアンサンブル」で作成した予測値の平均値です。
# テストデータでの予測
# plot_data関数へ送るデータ
plt_target = df_test_preds.iloc[:, 0]
plt_pred = df_test_preds.iloc[:, 1:].mean(axis=1)
plt_title = 'test preds'
plt_R2 = test_preds_ave_R2_score
plt_RMSE = test_preds_ave_RMSE_score
# plot_data関数でグラフを描画
plot_data(plt_target, plt_pred, plt_title, plt_R2, plt_RMSE)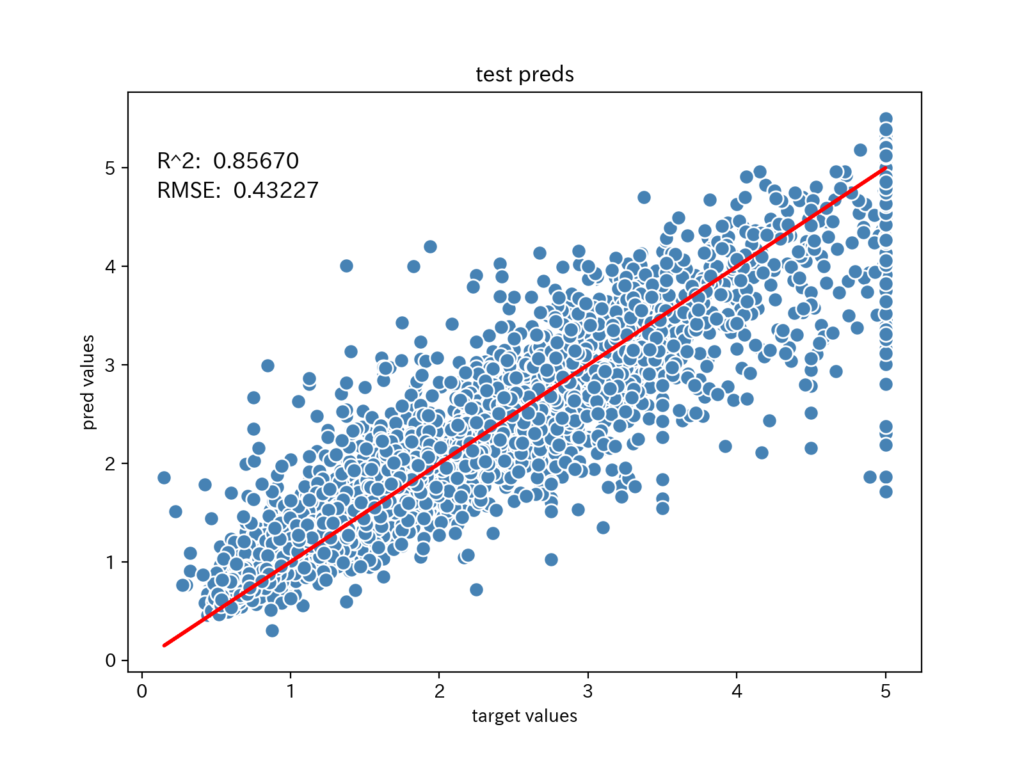
予測値は、赤い直線に沿っているものの、学習用データより誤差が大きくなっています。
しかし、検証用データより誤差が小さいので、アンサンブルの効果がでていることがわかります。
R^2やRMSEが、検証用データより良い値であることが、グラフに描くことで直感的に理解できます。
また、グラフを重ねて描くと、更に差分がよくわかるので、試してみてください。
まとめ
とても長い記事になってしまいました。
最後までご覧いただきありがとうございます。
今回は、前処理済みのデータセットを使用したので、LightGBMをとても簡単に使うことができ、それなりに良い精度のモデルを作ることができました。
しかし、生データやコンペで与えられるデータでは、簡単には良い精度が出せません。
データの前処理や予測値の検証に取り組み、少しずつモデルを改善していきますが、思うようにデータをハンドリングするのは難しいものです。
そのため、LightGBMの解説に比べ、Pandasでの操作に力を入れて解説しました。
どこかで役に立つTipsが紹介できていると、うれしいです。


