(その1)からの続きです。
(その2)からご覧の方のために、「特徴量の作成」まで(その1)と同じ内容を掲載しています。
課題の設定
異なるモデルを組み合わせると、個別に使用するよりも高い予測性能が得られることがあります。
この記事では、次の内容を解説します。
・多数決による予測(Voting)
・スタッキングによる予測(Stacking)
多数決による予測(Voting)とは
多数決による予測とは、各モデルの予測値で「多数決」を行う投票を行い、最も得票の多いクラスを予測値として選択します。
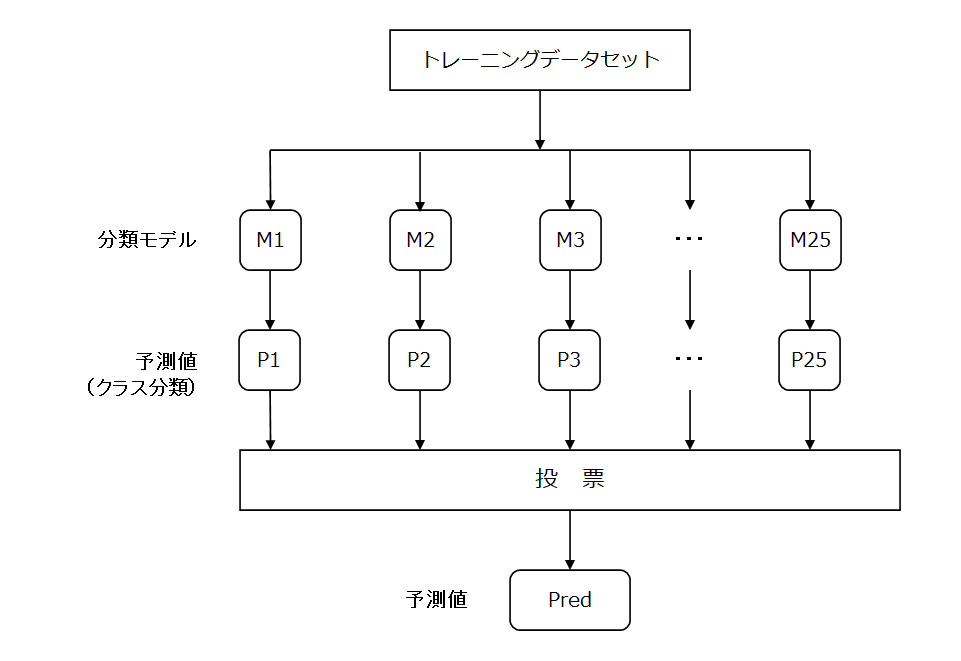
詳しくは、(その1)をご覧ください(新しいタブで開きます)。
【Python覚書】アンサンブル学習:XGBoost、LightGBM、CatBoostを組み合わせる(その1)
スタッキングによる予測(Stacking)とは
スタッキングによる予測とは、今回の例では、1段目の各モデルから得た予測値を特徴量して、2段目のモデルを学習させて予測値を得るものです。
モデルの組み合わせや積み上げ方は様々ですが、今回は2段のスタッキングを行ってみます。
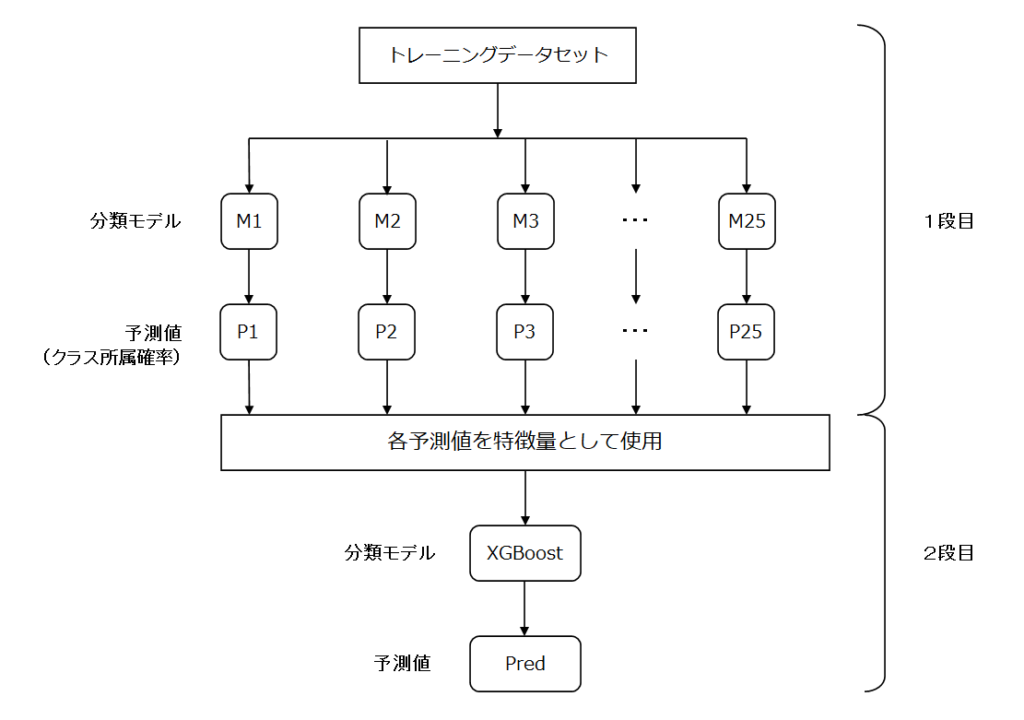
分析の流れ
データセットの読込からモデルでの予測まで、以下の作業をやってみます。
1段目は、LightGBMについてまとめた以下の記事と同じ流れです。
1段目のコード解説は、こちらをご覧ください(新しいタブで開きます)。
【Python覚書】LightGBMで交差検証を実装してみる
XGBoost、LightGBMのコード解説は、こちらをご覧ください。
【Python覚書】XGBoostで多値分類問題を解いてみる
【Python覚書】LigthGBMで多値分類問題を解いてみる
分析は、scikit-learnのwineデータセットを使用します。
- データセットの読み込み
<1段目: XGBoost、LightGBM、CatBoost> - 特徴量の作成
- パラメータの設定
- モデルの作成
- モデルの評価
<アンサンブル> - 多数決による予測<Voting> ※Votingは1段目まで
- スタッキングによる予測<2段目: XGBoost>
使用するライブラリ
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import xgboost as xgb
import lightgbm as lgb
from catboost import CatBoost
from catboost import Pool
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.model_selection import StratifiedKFold
from sklearn import datasetsXGBoost、LightGBM、CatBoostは、インストールされている前提でインポートしています。
データセット
# wine データセットを読み込む
wine = datasets.load_wine()
X = wine['data']
y = wine['target']
# 説明変数をpandas.DataFrameに入れ、カラム名を付ける
df_X = pd.DataFrame(X, columns=wine['feature_names'])sklearn.datasetsからwineデータセットを読み込みます。
説明変数 wine[‘data’]を変数X、目的変数 wine[‘target’]を変数yに格納しています。
さらに、変数Xを、各要素(特徴量)の名称 wine[‘feature_names’]をカラム名として、pandas.DataFrameに格納しています。
特徴量の作成
説明変数を確認します。
先頭の5行を取得します。
df_X.head()
表示が切れていますが、スクロールして確認できます。
なお、上の出力例は画像ですので、スクロールしません。
df_X.info()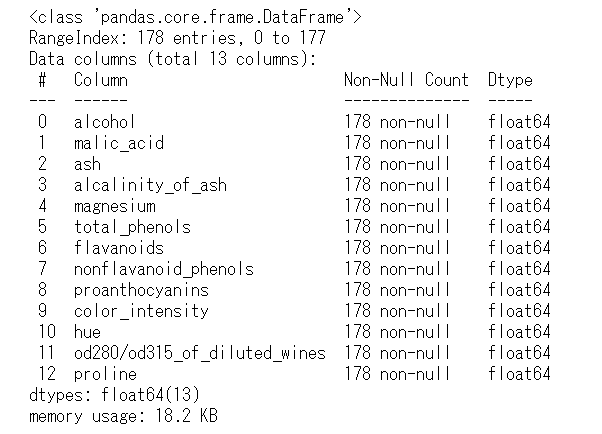
説明変数は、13個で、float64型の数値変数のみです。
その値は、連続する値の数値データで、カテゴリーやラベルを表すものはありません。
今回使用するXGBoost、LightGBM、CatBoostは、トレーニングデータセットの特徴量を標準化する必要はありませんが、その他の手法を使用するときのために、トレーニングデータセットの標準化(平均0、分散1)をしておきます。
# 説明変数を標準化
sc = StandardScaler()
X_std = sc.fit_transform(X)
# 説明変数をpandas.DataFrameに入れ、カラム名を付ける
df_X_std = pd.DataFrame(X_std, columns=wine['feature_names'])
df_X_std.head()
学習を難しくするため、13個の説明変数のうち、2個に絞ります。
以下は、XGBoostの学習させたfeature importance(特徴量の重要度)です。
今回は、上から4番目と5番目の特徴量を使用してみます。
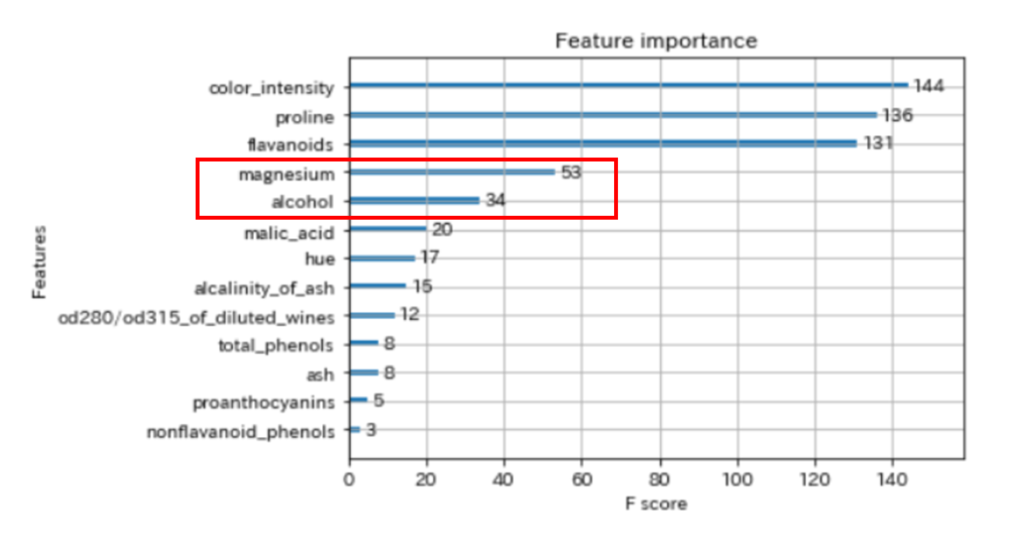
# 説明変数を2個に絞る
# 標準化する前と同じ変数名を再利用しているの、ご注意ください。
df_X = df_X_std[['magnesium', 'alcohol']]同じ名前の変数を再利用するのはよくないですが、横着します。
モデルの作成
スタッキングによる予測(Stacking)
2段のスタッキングによる予測を行います。
1段目は、2段目に使用する特徴量を作成します。
2段目は、1段目で作成した特徴量を使用して、目的変数の予測を行います。
1段目の概要
1段目の目的は、2段目に使用する特徴量を作成するために、説明変数の全データの予測値を得ることです。
いままでの記事では、ホールドアウト法を使って、データセット全体を3つに分割し、テストデータはモデルの評価として取り出していました。
スタッキングの1段目で、同じようにテストデータを取り出してしまうと、2段目で使用できるデータ量が少なくなってしまいます。
よって、以下のようにすべてのデータで交差検証(クロスバリデーション)を行い、説明変数の全データの予測値を得ます。
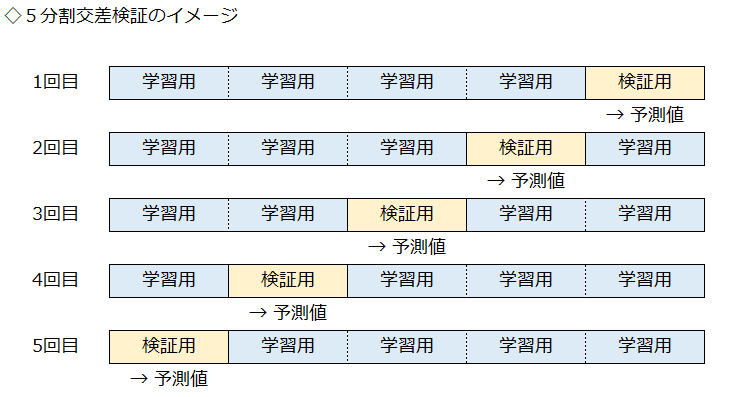
5分割交差検証を行うと、重複していない検証用データの予測値が得られます。
この予測値を1つに統合すると、説明変数の全データの予測値となります。
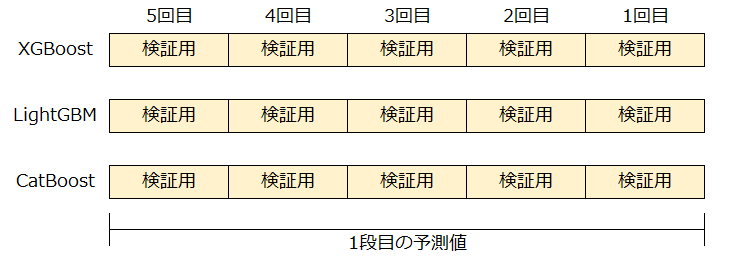
実際の予測値は、目的変数がそれぞれ0,1,2になる確率(合計1)を求めます。
これを、Pandas.DataFrameに保存すると、以下のようなデータになります。
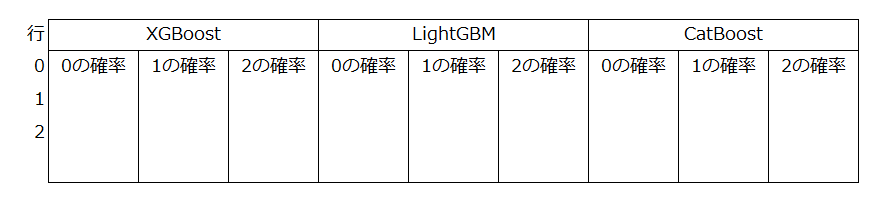
今回は、3種類のモデルを、5つのシード値で行い、出力は0から1の3クラスなので、全部で45列のデータを作成します。
それでは、モデルを作成していきましょう。
XGBoostの関数
def xgb_train_cv(X_train_cv, y_train_cv, X_eval_cv, y_eval_cv, loop_counts):
# データを格納する
# 学習用
xgb_train = xgb.DMatrix(X_train_cv, label=y_train_cv)
# 検証用
xgb_eval = xgb.DMatrix(X_eval_cv, label=y_eval_cv)
# テスト用
#xgb_test = xgb.DMatrix(X_test, label=y_test)
xgb_params = {
'objective': 'multi:softprob', # 多値分類問題
'num_class': 3, # 目的変数のクラス数
'learning_rate': 0.1, # 学習率
'eval_metric': 'mlogloss' # 学習用の指標 (Multiclass logloss)
}
# 学習
evals = [(xgb_train, 'train'), (xgb_eval, 'eval')] # 学習に用いる検証用データ
evaluation_results = {} # 学習の経過を保存する箱
bst = xgb.train(xgb_params, # 上記で設定したパラメータ
xgb_train, # 使用するデータセット
num_boost_round=200, # 学習の回数
early_stopping_rounds=10, # アーリーストッピング
evals=evals, # 学習経過で表示する名称
evals_result=evaluation_results, # 上記で設定した検証用データ
verbose_eval=0 # 学習の経過の表示(非表示)
)
# 検証用データで予測
y_pred = bst.predict(xgb_eval, ntree_limit=bst.best_ntree_limit)
y_pred_max = np.argmax(y_pred, axis=1)
print('Trial: ' + str(loop_counts))
# Accuracy の計算
accuracy = accuracy_score(y_eval_cv, y_pred_max)
print('XGBoost Accuracy:', accuracy)
return(bst, accuracy, y_pred)LightGBMの関数
def lgbm_train_cv(X_train_cv, y_train_cv, X_eval_cv, y_eval_cv):
# データを格納する
# 学習用
lgb_train = lgb.Dataset(X_train_cv, y_train_cv,
free_raw_data=False)
# 検証用
lgb_eval = lgb.Dataset(X_eval_cv, y_eval_cv, reference=lgb_train,
free_raw_data=False)
# パラメータを設定
params = {'task': 'train', # レーニング ⇔ 予測predict
'boosting_type': 'gbdt', # 勾配ブースティング
'objective': 'multiclass', # 目的関数:多値分類、マルチクラス分類
'metric': 'multi_logloss', # 検証用データセットで、分類モデルの性能を測る指標
'num_class': 3, # 目的変数のクラス数
'learning_rate': 0.1, # 学習率(初期値0.1)
'num_leaves': 23, # 決定木の複雑度を調整(初期値31)
'min_data_in_leaf': 1, # データの最小数(初期値20)
}
# 学習
evaluation_results = {} # 学習の経過を保存する箱
model = lgb.train(params, # 上記で設定したパラメータ
lgb_train, # 使用するデータセット
num_boost_round=200, # 学習の回数
valid_names=['train', 'valid'], # 学習経過で表示する名称
valid_sets=[lgb_train, lgb_eval], # モデルの検証に使用するデータセット
evals_result=evaluation_results, # 学習の経過を保存
early_stopping_rounds=10, # アーリーストッピングの回数
verbose_eval=0) # 学習の経過を表示する刻み(非表示)
# 検証用データで予測
y_pred = model.predict(X_eval_cv, num_iteration=model.best_iteration)
y_pred_max = np.argmax(y_pred, axis=1)
# Accuracy の計算
accuracy = accuracy_score(y_eval_cv, y_pred_max)
print('LightGBM Accuracy:', accuracy)
return(model, accuracy, y_pred)CatBoostの関数
def catboost_train_cv(X_train_cv, y_train_cv, X_eval_cv, y_eval_cv):
# データを格納する
# 学習用
CatBoost_train = Pool(X_train_cv, label=y_train_cv)
# 検証用
CatBoost_eval = Pool(X_eval_cv, label=y_eval_cv)
# パラメータを設定
params = {
'loss_function': 'MultiClass', # 多値分類問題
'num_boost_round': 1000, # 学習の回数
'early_stopping_rounds': 10 # アーリーストッピングの回数
}
# 学習
catb = CatBoost(params)
catb.fit(CatBoost_train, eval_set=[CatBoost_eval], verbose=False)
# 検証用データで予測
y_pred = catb.predict(X_eval_cv, prediction_type='Probability')
y_pred_max = np.argmax(y_pred, axis=1)
# Accuracy の計算
accuracy = sum(y_eval_cv == y_pred_max) / len(y_eval_cv)
print('CatBoost Accuracy:', accuracy)
return(catb, accuracy, y_pred)学習の実行
モデルの学習を行います。
1段目の大まかな流れは、以下のように2重ループをぐるぐる回します。
5分割の交差検証(クロスバリデーション)を行いますが、この分割のシード値を5回変えます。
ここで、2段目で使用する特徴量を作成します。
2段目は、1段目で作成した特徴量を使用して、単独のXGBoostのモデルを作成します。
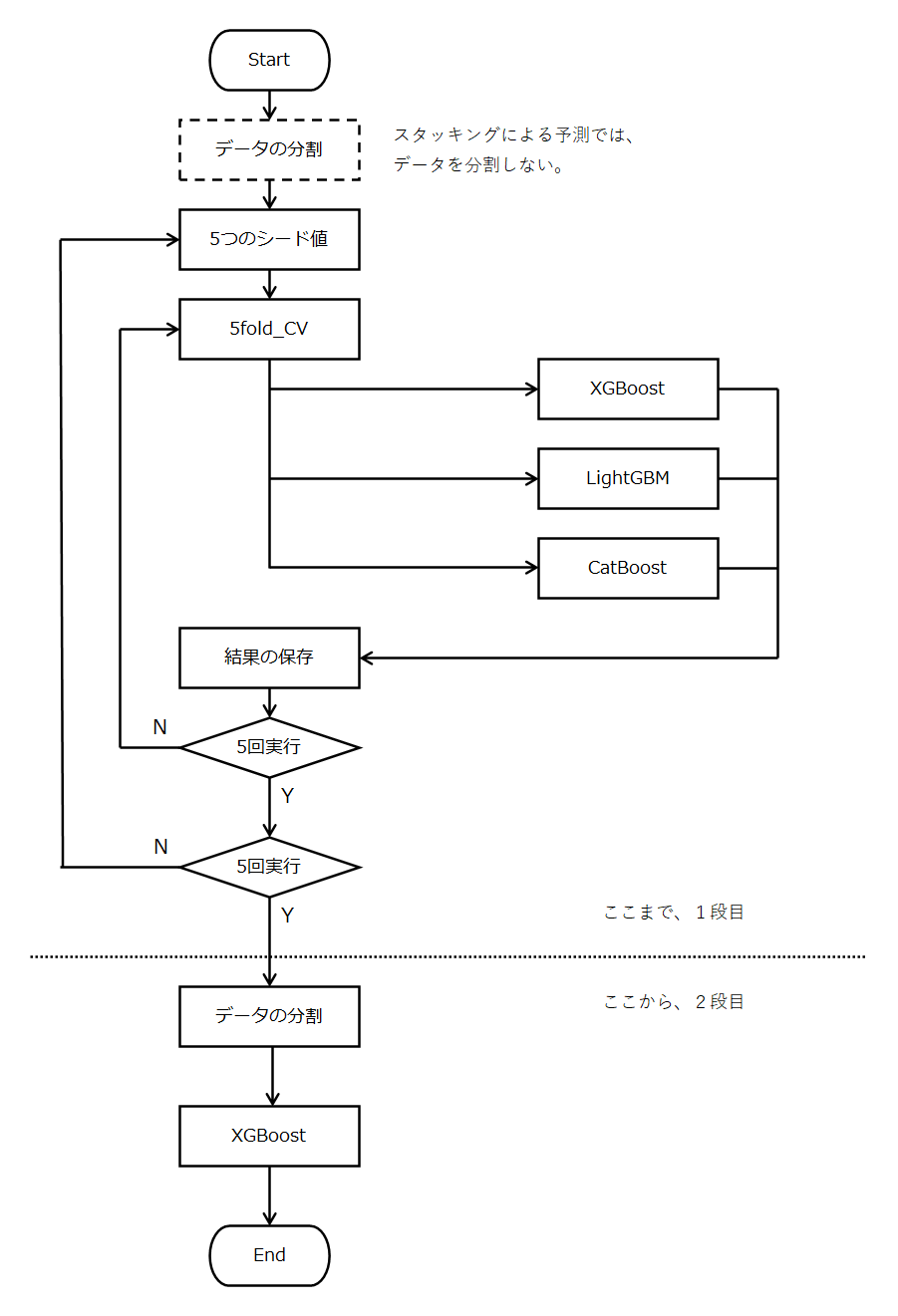
実際のコードは、以下の通りです。
# 各5つのモデルを保存するリストの初期化
xgb_models = []
lgbm_models = []
catb_models = []
# 各5つのモデルの正答率を保存するリストの初期化
xgb_accuracies = []
lgbm_accuracies = []
catb_accuracies = []
# 学習のカウンター
loop_counts = 1
# 各クラスの確率(3モデル*5seed*3クラス)
first_probs = pd.DataFrame(np.zeros((len(df_X), 3*5*3)))
for seed_no in range(5):
# 学習データの数だけの数列(0行から最終行まで連番)
row_no_list = list(range(len(df_X)))
# KFoldクラスをインスタンス化(これを使って5分割する)
K_fold = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)
# KFoldクラスで分割した回数だけ実行(ここでは5回)
for train_cv_no, eval_cv_no in K_fold.split(row_no_list, y):
# ilocで取り出す行を指定
X_train_cv = df_X.iloc[train_cv_no, :]
y_train_cv = pd.Series(y).iloc[train_cv_no]
X_eval_cv = df_X.iloc[eval_cv_no, :]
y_eval_cv = pd.Series(y).iloc[eval_cv_no]
# XGBoostの訓練を実行
bst, bst_accuracy, xgb_prob = xgb_train_cv(X_train_cv, y_train_cv,
X_eval_cv, y_eval_cv,
loop_counts)
# LIghtGBMの訓練を実行
model, model_accuracy, lgbm_prob = lgbm_train_cv(X_train_cv, y_train_cv,
X_eval_cv, y_eval_cv)
# CatBoostの訓練を実行
catb, catb_accuracy, catb_prob = catboost_train_cv(X_train_cv, y_train_cv,
X_eval_cv, y_eval_cv)
# 実行回数のカウント
loop_counts += 1
# 学習が終わったモデルをリストに入れておく
xgb_models.append(bst)
lgbm_models.append(model)
catb_models.append(catb)
# 学習が終わったモデルの正答率をリストに入れておく
xgb_accuracies.append(bst_accuracy)
lgbm_accuracies.append(model_accuracy)
catb_accuracies.append(catb_accuracy)
# 検証データの各クラスの確率
for i in range(3):
first_probs.iloc[eval_cv_no, (seed_no * 3) + i] = xgb_prob[:, i]
first_probs.iloc[eval_cv_no, (seed_no * 3) + 15 + i] = lgbm_prob[:, i]
first_probs.iloc[eval_cv_no, (seed_no * 3) + 30 + i] = catb_prob[:, i]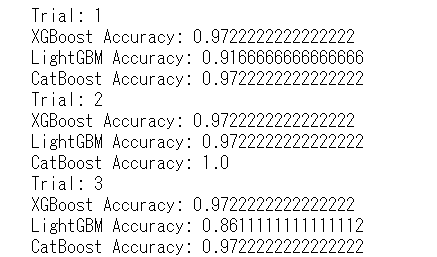
説明変数の全データの予測値を得ることできましたので、見てみましょう。
first_probs.head()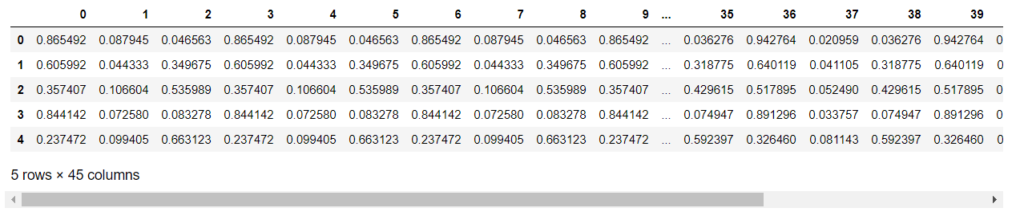
左から3列毎に1つのモデルの出力になっており、
左から0~14列がXGBoost、15~29列がLightGBM、30~44列がCatBoostの出力です。
単独のモデルの平均性能
モデルの平均性能を見てみましょう。
25個のモデル(5CV×5seed)について、それぞれの正答率(Accuracy)の平均値を算出します。
# 単独のモデルでの、テストデータの正答率
print('XGBoost Accuracy: ', np.array(xgb_accuracies).mean())
print('LightGBM Accuracy: ', np.array(lgbm_accuracies).mean())
print('CatBoost Accuracy: ', np.array(catb_accuracies).mean())XGBoost Accuracy: 0.6736507936507937
LightGBM Accuracy: 0.6680952380952381
CatBoost Accuracy: 0.7246031746031746(その1)の多数決による予測(Voting)のときと比べてみます。
| スタッキングによる予測 | 多数決による予測 | |
| 使用したデータ | 検証用データ | テストデータ |
XGBoost Accuracy: | 67.4% | 68.6% |
| LightGBM Accuracy: | 66.8% | 63.6% |
| CatBoost Accuracy: | 72.5% | 72.9% |
今回は、同じくらいの正答率となりましたが、その意味合いは違います。
多数決による予測は、ホールドアウト法で分割した未知のテストデータに対する正答率です。
一方、スタッキングによる予測は、学習には使用していませんが、学習時にモデル評価に使用している検証用データに対する正答率です。
検証用データの誤差が小さくなるように学習しているので、未知のデータに対しても同じ性能が発揮できるのか不安が残ります。
ブースティングによるモデルの評価をするときは、ホールドアウト法を使用した方が無難だと思います。
なお、スタッキングによる予測の1段目は、特徴量の抽出が目的なので、ここでの正答率はあまり気にしないでよいです。
多様性のある複数モデル
1段目は、特徴量の抽出が目的なので、多様性のある複数のモデルを使用したほうが2段目での良い結果が期待できます。
具体的には、
・モデルの種類を増やす(サポートベクターマシンやニューラルネットワークなど)
・モデルのパラメータを変える(決定木の深さ。ニューラルネットの構成など)
・使用する説明変数を変える など
今回は、シード値のみの変更なので、多様性という点ではあまり期待できないので、上記のような工夫を追加してみてください。
スタッキングによる予測の性能
スタッキングによる予測です。
2段目は、1段目で作成した特徴量を使用して、単独のXGBoostのモデルを作成します。
loop_counts = 0
# 学習データとテストデータに分ける
X_train, X_test, y_train, y_test = train_test_split(first_probs, y,
test_size=0.2,
random_state=0,
stratify=y)
# 予測結果の格納用のnumpy行列を作成
test_preds = np.zeros((len(y_test), 5))
# 学習データの数だけの数列(0行から最終行まで連番)
row_no_list = list(range(len(y_train)))
# KFoldクラスをインスタンス化(これを使って5分割する)
K_fold = StratifiedKFold(n_splits=5, shuffle=True, random_state=0)
# KFoldクラスで分割した回数だけ実行(ここでは5回)
for train_cv_no, eval_cv_no in K_fold.split(row_no_list, y_train):
# ilocで取り出す行を指定
X_train_cv = X_train.iloc[train_cv_no, :]
y_train_cv = pd.Series(y_train).iloc[train_cv_no]
X_eval_cv = X_train.iloc[eval_cv_no, :]
y_eval_cv = pd.Series(y_train).iloc[eval_cv_no]
# データを格納する
# 学習用
xgb_train = xgb.DMatrix(X_train_cv, label=y_train_cv)
# 検証用
xgb_eval = xgb.DMatrix(X_eval_cv, label=y_eval_cv)
# テスト用
xgb_test = xgb.DMatrix(X_test, label=y_test)
xgb_params = {
'objective': 'multi:softprob', # 多値分類問題
'num_class': 3, # 目的変数のクラス数
'learning_rate': 0.1, # 学習率
'eval_metric': 'mlogloss' # 学習用の指標 (Multiclass logloss)
}
# 学習
evals = [(xgb_train, 'train'), (xgb_eval, 'eval')] # 学習に用いる検証用データ
evaluation_results = {} # 学習の経過を保存する箱
bst = xgb.train(xgb_params, # 上記で設定したパラメータ
xgb_train, # 使用するデータセット
num_boost_round=200, # 学習の回数
early_stopping_rounds=10, # アーリーストッピング
evals=evals, # 学習経過で表示する名称
evals_result=evaluation_results, # 上記で設定した検証用データ
verbose_eval=0 # 学習の経過の表示(非表示)
)
y_pred = bst.predict(xgb_test, ntree_limit=bst.best_ntree_limit)
y_pred_max = np.argmax(y_pred, axis=1)
# testの予測を保存
test_preds[:, loop_counts] = y_pred_max
print('Trial: ' + str(loop_counts))
loop_counts += 1
acc = accuracy_score(y_test, y_pred_max)
print('Accuracy:', acc)Trial: 0
Accuracy: 0.6666666666666666
Trial: 1
Accuracy: 0.6944444444444444
Trial: 2
Accuracy: 0.7777777777777778
Trial: 3
Accuracy: 0.75
Trial: 4
Accuracy: 0.7777777777777778モデルの評価
5分割の交差検証(クロスバリデーション)を行いましたので、5つのモデルでの多数決による予測の性能を見てみます。
# 予測したクラスのデータをpandas.DataFrameに入れる
df_test_preds = pd.DataFrame(test_preds)
# 5つの予測の格納用のnumpy行列を作成
test_preds_max = np.zeros((len(y_test), 3))
# 各列(0,1,2)に、そのクラスを予測したモデルの数を入れる
test_preds_max[:, 0] = (df_test_preds == 0).sum(axis=1)
test_preds_max[:, 1] = (df_test_preds == 1).sum(axis=1)
test_preds_max[:, 2] = (df_test_preds == 2).sum(axis=1)
# 各行で、そのクラスを予測したモデルの数が最も多いクラスを得る
pred_max = np.argmax(test_preds_max, axis=1)
# Accuracy を計算する
accuracy = sum(y_test == pred_max) / len(y_test)
print('accuracy:', accuracy)
df_accuracy = pd.DataFrame({'va_y': y_test,
'y_pred_max': pred_max})
print(pd.crosstab(df_accuracy['va_y'], df_accuracy['y_pred_max']))
1段目の正答率や、(その1)の多数決による予測での正答率75.0%よりも良い正答率になりました。
留意しておく点としては、学習データとテストデータに分けるときのシード値を変更するだけで、正答率は上下します。
モデルの比較をするときは、同じシード値でデータを分割する必要があります。
ちなみに、1段目で作成した特徴量を(その1)のモデルに使用してみると、以下のような結果になりました。

奇しくも、(その1)の多数決による予測75.0%と同じ正答率です。
ただし、誤答の仕方は違っているので、比較してみてください。
まとめ
大変長くなってしまいましたが、XGBoost、LightGBM、CatBoostを組み合わせたアンサンブル学習を行いました。
ブースティング(XGBoost、LightGBM、CatBoost)自体が、弱学習器を統合する「アンサンブル学習」なので、表現が紛らわしいですが、この記事では、XGBoost、LightGBM、CatBoostを2つの方法(Voting、Stacking)で組み合わせています。
計算量の増加に見合った成果があるとは限りませんが、ぎりぎりまで精度の向上を図るには有効な方法だと思います。


